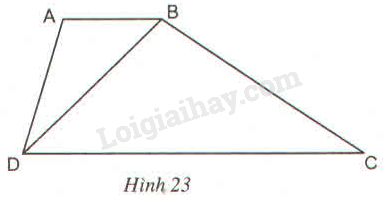
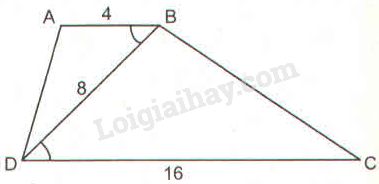
Bài 36 trang 92 SBT toán 8 tập 2

Đề bài

Hình thang $ABCD \;(AB // CD)$ có $AB = 4cm, CD = 16cm$ và $BD = 8cm$ (h23).

Chứng minh $\widehat {BAD} = \widehat {DBC}$ và $BC = 2 AD.$ 

Lời giải chi tiết

Ta có: 

$\eqalign{  & {{AB} \over {BD}} = {4 \over 8} = {1 \over 2}  \cr  & {{BD} \over {DC}} = {8 \over {16}} = {1 \over 2} \cr}$

$\Rightarrow\displaystyle {{AB} \over {BD}} = {{BD} \over {DC}} = {1 \over 2}$

Vì $AB//CD$ (gt) nên $\widehat {ABD} = \widehat {BDC}$ (cặp góc so le trong)

Xét $∆ ABD$ và $∆ BDC$ có:

$\widehat {ABD} = \widehat {BDC}$ (chứng minh trên)

$\displaystyle{{AB} \over {BD}} = {{BD} \over {DC}}$ (chứng minh trên)

$\Rightarrow ∆ ABD$ đồng dạng $∆ BDC$ (c.g.c)

$\Rightarrow \widehat {BAD} = \widehat {DBC}$ (hai góc tương ứng).

Tỉ số đồng dạng $\displaystyle  k = {AB \over BD}= {1 \over 2}$.

$\Rightarrow\displaystyle  {{AD} \over {BC}} = {1 \over 2} \Rightarrow BC = 2AD$ (đpcm).

HocTot.Nam.Name.Vn