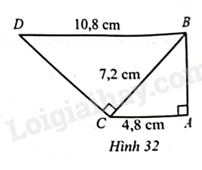
Giải bài 36 trang 72 sách bài tập toán 8 – Cánh diều

Đề bài

Quan sát Hình 32 có $\widehat {BAC} = 90^\circ ,\widehat {BCD} = 90^\circ ,DB = 10,8$cm, $BC = 7,2$cm và $CA = 4,8$cm. Chứng minh: $\Delta DBC\backsim \Delta BCA$.

Lời giải chi tiết

Nhận thấy: $\frac{{DB}}{{CB}} = \frac{{10,8}}{{7,2}} = \frac{3}{2},\frac{{BC}}{{CA}} = \frac{{7,2}}{{4,8}} = \frac{3}{2}$. Từ đó ta có: tam giác $DBC$ vuông tại đỉnh $C$, tam giác $BCA$ vuông tại đỉnh $A$ và $\frac{{DB}}{{CB}} = \frac{{BC}}{{CA}}$ (vì cùng bằng $\frac{3}{2}$). Suy ra $\Delta DBC\backsim \Delta BCA$.