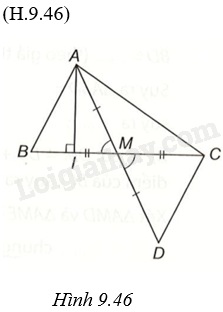
Giải bài 3 (9.38) trang 87 vở thực hành Toán 7 tập 2Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng: a) (AI < frac{1}{2}left( {AB + AC} right)); b) (AM < frac{1}{2}left( {AB + AC} right)). Đề bài Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng: a) \(AI < \frac{1}{2}\left( {AB + AC} \right)\); b) \(AM < \frac{1}{2}\left( {AB + AC} \right)\). Phương pháp giải - Xem chi tiết a) Chứng minh \(AI < AB\), \(AI < AC\) nên \(2AI < AB + AC\) hay \(AI < \frac{1}{2}\left( {AB + AC} \right)\). b) + Lấy điểm D sao cho M là trung điểm của AD. + Chứng minh \(\Delta ABM = \Delta DCM\left( {c.g.c} \right)\), suy ra \(AB = CD\). + Chỉ ra \(AD < AC + DC\), suy ra \(2AM < AC + AB\), suy ra \(AM < \frac{1}{2}\left( {AB + AC} \right)\) Lời giải chi tiết
a) Trong tam giác vuông AIB có AB là cạnh huyền nên \(AI < AB\). Trong tam giác vuông AIC có AC là cạnh huyền nên \(AI < AC\). Suy ra \(2AI < AB + AC\) hay \(AI < \frac{1}{2}\left( {AB + AC} \right)\). b) Lấy điểm D sao cho M là trung điểm của AD. Xét \(\Delta ABM\) và \(\Delta DCM\) có: \(AM = MD,\widehat {AMB} = \widehat {DMC},MB = MC\), do đó, \(\Delta ABM = \Delta DCM\left( {c.g.c} \right)\). Trong tam giác ACD, ta có \(AD < AC + DC\), suy ra \(2AM < AC + AB\), suy ra \(AM < \frac{1}{2}\left( {AB + AC} \right)\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
