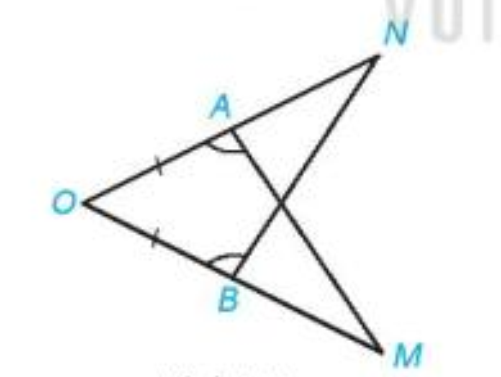
Giải bài 3 (4.35) trang 79 vở thực hành Toán 7Bài 3 (4.35). Trong hình vẽ sau ta có AO = BO, \(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN. Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Bài 3 (4.35). Trong hình vẽ sau ta có AO = BO, \(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
Phương pháp giải - Xem chi tiết Chứng minh hai tam giác AOM và BON bằng nhau. Lời giải chi tiết Xét hai tam giác AOM và BON ta có: \(\widehat {OAM} = \widehat {OBN}\), OA = OB (theo giả thiết) \(\widehat {AOM} = \widehat {BON}\)(góc chung) Vậy \(\Delta AOM = \Delta BON\)(g-c-g). Do đó AM = BN.
|