Bài 2.9, 2.10, 2.11 phần bài tập bổ sung trang 109 SBT toán 9 tập 1Giải bài 2.9, 2.10, 2.11 phần bài tập bổ sung trang 109 sách bài tập toán 9. tìm đẳng thức đúng trong các bài...
Lựa chọn câu để xem lời giải nhanh hơn
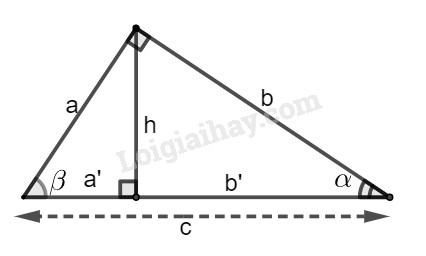
Xét hình bs. 4. Tìm đẳng thức đúng trong các bài từ 2.9 đến 2.11.
Bài 2.9 (A) \({\cos ^2}\alpha + {\sin ^2}\beta = 1\); (B) \({\sin ^2}\alpha + {\cos ^2}\beta = 1\) ; (C) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) ; (D) \({\cos ^2}\alpha + {\cos ^2}\beta = 2\). Phương pháp giải: Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
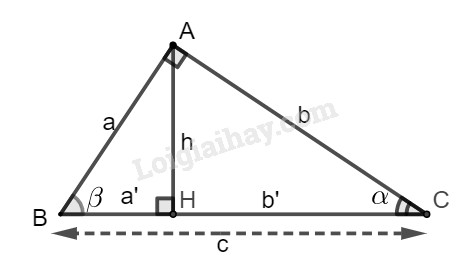
\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\) Lời giải chi tiết: Đặt tên hình như hình sau (hình vẽ được sử dụng cho các bài 2.9, 2.10 và 2.11):
Xét tam giác ABC vuông tại A, ta có: \(a^2+b^2=c^2\) (định lý Pytago) và: \(\begin{array}{l} Vậy đáp án là (C) Bài 2.10 (A) \(tg\alpha = \sin\alpha + \cos\alpha\) ; (B) \(tg\alpha = \sin\alpha - \cos\alpha\) ; (C) \(tg\alpha = \sin\alpha .\cos\alpha\) ; (D) \(tg \alpha\) = \(\dfrac{{\sin \alpha }}{{\cos \alpha }}.\) Lời giải chi tiết: \(\begin{array}{l} Vậy đáp án (D) Bài 2.11 (A) \(cotg\alpha = 1 + tg\alpha\); (B) \(cotg\alpha = 1 − tg\alpha\); (C) \(cotg\alpha = 1.tg\alpha\) ; (D) \(cotg\alpha = \dfrac{1}{{tg\alpha }}.\) Lời giải chi tiết: \(\begin{array}{l} Vậy đáp án là (D). HocTot.Nam.Name.Vn
|