Bài 2.16 phần bài tập bổ sung trang 110 SBT toán 9 tập 1

Đề bài

Cho tam giác \(ABC\) có \(\widehat A = 60^\circ \). Chứng minh rằng:

\(BC^2 = AB^2 + AC^2 – AB.AC.\)

Lời giải chi tiết

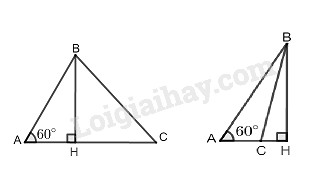
Kẻ đường cao \(BH\) của tam giác \(ABC\) thì \(H\) nằm trên tia \(AC\) (để \(\widehat {BAC} = 60^\circ \) là góc nhọn ), do đó \(HC^2 = (AC – AH)^2\) 

Theo định lý Pytago trong tam giác vuông BHC, ta có:

\(\begin{array}{l}
B{C^2} = B{H^2} + H{C^2}\\
= B{H^2} + \left( {A{C} - A{H}} \right)^2\\
= B{H^2} + A{H^2} + A{C^2} - 2AC.AH\\
= A{B^2} + A{C^2} - 2AC.AH
\end{array}\)

Xét tam giác ABH có \(\widehat {BAC} = 60^\circ \), theo định nghĩa tỉ số lượng giác của góc nhọn ta có:

\(\cos A = \dfrac{{AH}}{{AB}}\) nên \(AH = AB \cos60^0 \) \(=\dfrac{{AB}}{ 2}\) 

Suy ra \(BC^2 =A{B^2} + A{C^2} - 2AC.\dfrac{{AB}}{ 2}\)\(= AB^2 + AC^2 – AB.AC.\)  

HocTot.Nam.Name.Vn