Bài 2.17 phần bài tập bổ sung trang 110 SBT toán 9 tập 1

Đề bài

Cho tứ giác \(ABCD\) có \(α\) là góc nhọn tạo bởi hai đường chéo chứng minh rằng:

\({S_{ABCD}} = \dfrac{1}{2}AC.BD.\sin a.\)   

Lời giải chi tiết

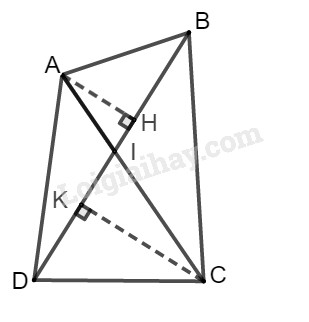
Giả sử hai đường chéo \( AC, BD\) cắt nhau tại \(I\), \(\widehat {AIB} = \alpha \) là góc nhọn.

Kẻ đường cao \(AH\) của tam giác \(ABD\) và đường cao \(CK\) của tam giác \(CBD\).

Xét tam gác AHI vuông tại H ta có: \(\sin \widehat {AIH} = \dfrac{{AH}}{{AI}} \Rightarrow AH = AI.\sin \alpha \)

Lại có \(\widehat {DIC} = \widehat {AIB} = \alpha \) (hai góc đối đỉnh)

Xét tam gác CKI vuông tại I ta có: \(\sin \widehat {CIK} = \dfrac{{CK}}{{CI}} \Rightarrow CK = CI.\sin \alpha \)

Diện tích tam giác \(ABD\) là \({S_{ABD}} = \dfrac{1}{2}BD.AH,\) 

Diện tích tam giác \(CBD\) là: \({S_{CBD}} = \dfrac{1}{ 2}BD.CK.\)

Từ đó diện tích \(S\) của tứ giác\( ABCD\) là:

\(\eqalign{
& S = {S_{ABD}} + {S_{CBD}} \cr 
& = {1 \over 2}BD.(AH + CK) \cr & = {1 \over 2}BD.(AI.\sin \alpha + CI.\sin \alpha) \cr
& = {1 \over 2}BD.(AI + CI).\sin \alpha \cr 
& = {1 \over 2}{\rm{BC}}{\rm{.AC.s}}in\alpha \cr} \)

HocTot.Nam.Name.Vn