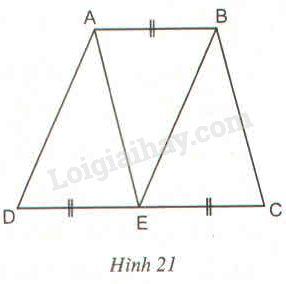
Bài 28 trang 90 SBT toán 8 tập 2

Đề bài

Hình thang \(ABCD\; (AB // CD)\) có \(CD = 2AB.\) Gọi \(E\) là trung điểm của \(DC\) (h21). Chứng minh rằng ba tam giác \(ADE, ABE\) và \(BEC\) đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau).

Lời giải chi tiết

Vì \(CD = 2AB\) (gt) nên \(\displaystyle AB  = {1 \over 2}CD\).

Vì \(E\) là trung điểm của \(CD\) nên \(\displaystyle DE = EC  = {1 \over 2}CD\)

\( \Rightarrow  AB = DE = EC\).

Xét tứ giác \(ABCE \) có \(AB//EC\) và \(AB = EC\) nên \(ABCE\) là hình bình hành.

\( \Rightarrow AE//BC\) (tính chất hình bình hành).

Vì \(AB//DC\) nên \(\widehat {ABE} = \widehat {BEC}\) (cặp góc so le trong).

Vì \(AE//BC\) nên \(\widehat {AEB} = \widehat {EBC}\) (cặp góc so le trong).

Xét \(∆ AEB\) và \(∆ CBE\) có:

\(\widehat {ABE} = \widehat {BEC}\) (cmt)

\(\widehat {AEB} = \widehat {EBC}\) (cmt)

\(BE \) cạnh chung

\(⇒ ∆ AEB = ∆ CBE\; (g.c.g)\)     (1)

Hình thang \(ABED\) có đáy \(AB = DE\) nên hai cạnh bên \(AD\) và \(BE\) song song với nhau.

Vì \(AB//CD\) nên \(\widehat {BAE} = \widehat {AED}\) (cặp góc so le trong).

Vì \(AD//BE\) nên \(\widehat {AEB} = \widehat {EAD}\) (cặp góc so le trong).

Xét \(∆ AEB\) và \(∆ EAD\) có:

\(\widehat {BAE} = \widehat {AED}\) (cmt)

\(\widehat {AEB} = \widehat {EAD}\) (cmt)

\(AE\) cạnh chung

\(⇒ ∆ AEB = ∆ EAD \;(g.c.g)\)    (2)

Từ (1) và (2) suy ra: \(∆ AEB = ∆ EAD = ∆ CBE\).

Do đó ba tam giác \(ADE, ABE\) và \(BEC \) đồng dạng với nhau từng đôi một.

HocTot.Nam.Name.Vn