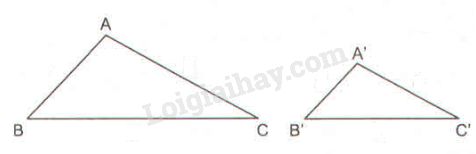
Bài 25 trang 89 SBT toán 8 tập 2

Đề bài

Cho hai tam giác \(A’B’C’\) và \(ABC\) đồng dạng với nhau theo tỉ số \(k.\) Chứng minh rằng tỉ số chu vi của hai tam giác cũng bằng \(k.\)

Lời giải chi tiết

Vì \(∆ A’B’C’\) đồng dạng \(∆ ABC\) theo tỉ số \(k\) nên ta có:

\(\displaystyle {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}} = k\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\displaystyle {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}} \)\(\,\displaystyle= {{A'B' + A'C' + B'C'} \over {AB + AC + BC}}\)

\( \Rightarrow \displaystyle {{A'B' + A'C' + B'C'} \over {AB + AC + BC}} = k\)

Vậy \(\dfrac{{{C_{A'B'C'}}}}{{{C_{ABC}}}} = k\).

Trong đó: \(C_{A'B'C'}\) là chu vi \(\Delta A'B'C'\).

                \(C_{ABC}\) là chu vi \(\Delta ABC\).

HocTot.Nam.Name.Vn