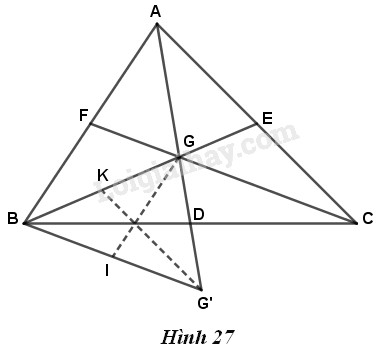
Bài 28 trang 79 Vở bài tập toán 7 tập 2Giải bài 28 trang 79 VBT toán 7 tập 2. Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’. a) So sánh các cạnh... Đề bài Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G′ sao cho G là trung điểm của AG′. (h.27) a) So sánh các cạnh của tam giác BGG′ với các đường trung tuyến của tam giác ABC. b) So sánh các đường trung tuyến của tam giác BGG′ với các cạnh của tam giác ABC.
Phương pháp giải - Xem chi tiết Áp dụng tính chất đường trung tuyến của tam giác. Lời giải chi tiết a) So sánh các cạnh của tam giác BGG′ với các đường trung tuyến của tam giác ABC. Theo tính chất trọng tâm của tam giác, ta có : BG=23BE, CG=23CF, AG=23AD. Mặt khác, do G là trung điểm của AG′ nên GG′=AG=23AD. Ta còn có ΔBDG′=ΔCDG (c.g.c), suy ra BG′=CG=23CF. Tóm lại ta có GG′=23AD; BG=23BE; BG′=23CF. b) So sánh các đường trung tuyến BD,GI,G′K của tam giác BGG′ với các cạnh của tam giác ABC. Ta có BD=12BC (vì D là trung điểm của BC). Hai tam giác AEG và G′KG có AG=GG′ vì G là trung điểm của AG′, GK=GE vì cùng bằng 13BE và ^AGE=^G′GK (đối đỉnh). Vậy ΔAEG=ΔG′KG, do đó G′K=AE=12AC (vì E là trung điểm của AC). Hai tam giác BDG′ và CDG bằng nhau theo câu a) nên ta có ^G′BD=^GCD, suy ra BG′//CF, do đó ^FGB=^GBI (so le trong). Hơn nữa, BG′=CG (=23CF) suy ra BI=12BG′=12CG=GF. Vậy ΔBFG=ΔGIB(c.g.c), suy ra GI=BF=12AB. Tóm lại BD=12BC; GI=12AB; G′K=12AC. HocTot.Nam.Name.Vn
|