SBT Toán 9 - giải SBT Toán 9 - Cánh diều

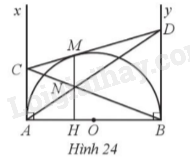
Giải bài 24 trang 109 sách bài tập toán 9 - Cánh diều tập 1

Cho nửa đường tròn tâm O đường kính AB, kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyển thứ ba cắt Ax, By lần lượt tại C, D. Gọi N là giao điểm của AD và BC và H là giao điểm của MN và AB (Hình 24).

Tổng hợp Đề thi vào 10 có đáp án và lời giải

Toán - Văn - Anh

Đề bài

Chứng minh:

a) $MN \bot AB$

b) $MN = NH$

Phương pháp giải - Xem chi tiết

a) Bước 1: Chứng minh $AC = CM,BD = DM$

Bước 2: Áp dụng định lý Thales trong các tam giác ANC, ACD để suy ra $\frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}$

b) Áp dụng định lý Thales trong các tam giác CAD, CAN, CBA suy ra $\frac{{MN}}{{AC}} = \frac{{NH}}{{CA}}$

Lời giải chi tiết

a) Ta có $Ax \bot AB,By \bot AB$ (do Ax, By là tiếp tuyến của (O)) nên $Ax//By$ .

Mặt khác, do Ax, By, CD là tiếp tuyến của (O)) nên $AC = CM,BD = DM$ .

Xét tam giác ANC có $AC//BD$ , áp dụng định lý Thales ta được $\frac{{NA}}{{ND}} = \frac{{AC}}{{BD}}$

nên $\frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}$ .

Xét tam giác CAD có $\frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}$ $\left( {N \in AD,M \in CD} \right)$ do đó $MN//AC$ .

Mà $AC \bot AB$ suy ra $MN \bot AB$ .

b) Áp dụng định lý Thales trong:

Tam giác CAD có $MN//AC$ : $\frac{{MN}}{{AC}} = \frac{{DN}}{{AD}}$ (1)

Tam giác CAN có $CA//BD$ : $\frac{{DN}}{{AD}} = \frac{{BN}}{{CB}}$ (2)

Tam giác CBA có $NH//CA$ : $\frac{{BN}}{{CB}} = \frac{{NH}}{{CA}}$ (3)

Từ (1), (2), (3) suy ra $\frac{{MN}}{{AC}} = \frac{{NH}}{{CA}}$ , do đó $MN = NH$

Chia sẻ

Bình luận

Bình chọn:

3.8 trên 6 phiếu

Giải bài 25 trang 109 sách bài tập toán 9 - Cánh diều tập 1
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A với $R \ne r$ . Đường nối OO' lần lượt cắt hai đường tròn (O) và (O’) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O') tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh: a) $\widehat {DME} = 90^\circ$ b) MA tiếp xúc với hai đường tròn (O) và (O') c) MD. MB=ME. MC
Giải bài 26 trang 110 sách bài tập toán 9 - Cánh diều tập 1
Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O') là đường tròn đường kính HC. Chứng minh: a) Điểm D thuộc đường tròn (O) và điểm E thuộc đường tròn (O’); b) Hai đường tròn (O) và (O') tiếp xúc ngoài; c) AH là tiếp tuyến chung của hai đường tròn (O) và (O’); d) AH = DE; e) Diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
Giải bài 23 trang 109 sách bài tập toán 9 - Cánh diều tập 1
Hình 23 minh họa thước phân giác. Thước gồm hai thanh gỗ ghép lại thành góc vuông BAC và một tấm gỗ có dạng hình tam giác ACD với AD là tia phân giác của góc BAC. Có thể dùng thước phân giác để tìm tâm của một hình tròn hay không? Vì sao?
Giải bài 22 trang 109 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; R) và điểm A nằm trên đường tròn. Lấy điểm B sao cho A là trung điểm của đoạn thẳng OB. Kẻ hai tiếp tuyến BM, BN của đường tròn (O). a) Tính số đo góc MBN và độ dài đoạn thẳng BM theo R. b) Tứ giác AMON là hình gì ? Vì sao? c) Tính độ dài đoạn thẳng OH theo R với H là giao điểm của OA và MN.
Giải bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC, sao cho $\widehat {CAB} = 30^\circ$ . Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh a) MC là tiếp tuyến của đường tròn (O). b) $MC = R\sqrt 3$ .

Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10