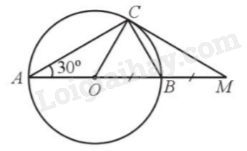
Giải bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC, sao cho ^CAB=30∘. Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh a) MC là tiếp tuyến của đường tròn (O). b) MC=R√3. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC, sao cho ^CAB=30∘. Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh a) MC là tiếp tuyến của đường tròn (O). b) MC=R√3. Phương pháp giải - Xem chi tiết a) Bước 1: Chứng minh CB=OB=BM. Bước 2: Dựa vào tính chất: Trong một tam giác, đường trung tuyến ứng với một cạnh và bằng nửa cạnh ấy thì tam giác đó vuông, ta chứng minh được CM⊥OC. b) Áp dụng tỉ số lượng giác trong tam giác vuông OCM để tính CM. Lời giải chi tiết
a) Xét tam giác OAC có OA=OC(=R) nên tam giác OAC cân tại O, do đó ˆA=^ACO=30∘. Xét tam giác ABC có OA=OB=OC=AB2(=R) nên tam giác ABC vuông tại C, nên ^ACB=90∘. Ta có ^ACO+^OCB=^ACB=90∘, suy ra ^OCB=90∘−^ACO=90∘−30∘=60∘. Xét tam giác OCB có OB=OC(=R) và ^OCB=60∘ nên tam giác OCB đều, do đó OC=OB=CB. Vậy OC=OB=CB=BM. Xét tam giác OCM có MB=OB=CB=OM2 nên tam giác OCM vuông tại C, hay CM⊥OC. Do đó MC là tiếp tuyến của đường tròn (O). b) Do tam giác OCM vuông tại C và ^COB=60∘ nên ˆM=30∘ Ta có tanM=OCMC hay MC=OCtanM=Rtan30∘=R√3.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|
