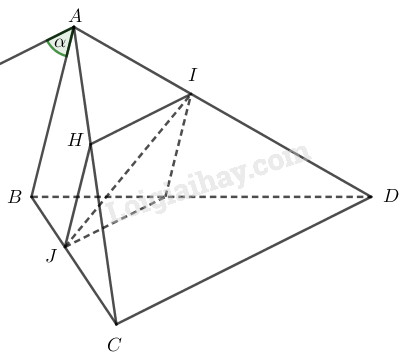
Bài 2.30 trang 78 SBT hình học 11Giải bài 2.30 trang 78 sách bài tập hình học 11. Cho tứ diện ABCD. Gọi I và J lần lượt là hai điểm di động trên các cạnh AD và BC sao cho... Đề bài Cho tứ diện ABCD. Gọi I và J lần lượt là hai điểm di động trên các cạnh AD và BC sao cho IAID=JBJC. Chứng minh rằng IJ luôn luôn song song với một mặt phẳng cố định. Phương pháp giải - Xem chi tiết Sử dụng định lý talet. Sử dụng tính chất: Nếu đường thẳng d không năm trong mặt phẳng (α) và d song song với đường thẳng d′ nằm trong (α) thì d song song với (α). {d⊄(α)d∥d′d′⊂(α)⇒d∥(α) Sử dụng tính chất khi (α) song song với (β) thì (α) sẽ song song với mọi đường thẳng nằm trong (β). Quảng cáo  Lời giải chi tiết
Qua I kẻ đường thẳng song song với CD cắt AC tại H nên ta có: HAHC=IAID. Mà IAID=JBJC. Từ đó suy ra HAHC=JBJC. Theo định lý Talet suy ra HJ∥AB mà HJ⊂(IJH) ⇒AB∥(IJH) (1) Theo cách dựng IH∥CD, IH⊂(IJH) ⇒CD∥(IJH) (2) Từ (1) và (2) suy ra (IJH)∥AB,CD. Gọi (α) là mặt phẳng đi qua AB và song song với CD. Ta có: {(α)∥(IJH)IJ⊂(IJH)⇒IJ∥(α) Vậy IJ song song với mặt phẳng (α) cố định. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
