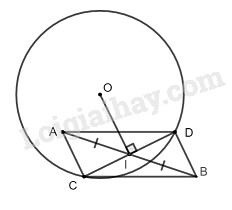
Bài 23 trang 159 SBT toán 9 tập 1Giải bài 23 trang 159 sách bài tập toán 9. Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. hãy cho biết ACBD là hình gì? Vì sao? Đề bài Cho đường tròn (O), điểm \(A\) nằm bên trong đường tròn, điểm \(B\) nằm ngoài đường tròn sao cho trung điểm \(I\) của \(AB\) nằm bên trong đường tròn. Vẽ dây \(CD\) vuông góc với \(OI\) tại \(I.\) hãy cho biết \(ACBD\) là hình gì? Vì sao? Phương pháp giải - Xem chi tiết + Tứ giác có các đường chéo cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình bình hành. + Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. Lời giải chi tiết
Xét đường tròn tâm O có: \(OI ⊥ CD\) (gt) mà OI là 1 phần đường kính, CD là dây của đường tròn Suy ra: \(IC = ID\) (đường kính vuông góc với dây thì đi qua trung điểm dây đó) Mà: \(IA = IB\) (vì I là trung điểm của AB) Tứ giác \(ACBD\) có hai đường chéo AB và CD cắt nhau tại trung điểm I của mỗi đường nên nó là hình bình hành. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
