Bài 2.1, 2.2, 2.3, 2.4 phần bài tập bổ sung trang 109 SBT toán 9 tập 1

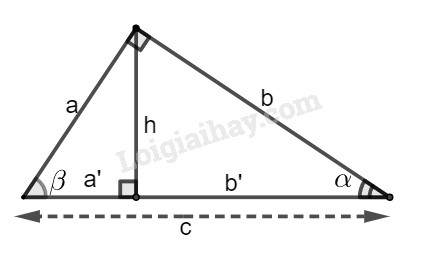
Bài 2.1

Xét hình bs. 4. Tìm đẳng thức đúng trong các bài từ 2.1 đến 2.11.

(A) \(\sin \alpha  = \dfrac{a}{ b}\); 

(B) \(\sin\alpha  = \dfrac{b}{c}\);

(C) \(\sin \alpha  = \dfrac{{b'}}{ b}\);

(D) \(\sin \alpha  = \dfrac{h}{b}.\) 

Phương pháp giải:

Sử dụng:  \(\sin \alpha  = \dfrac{{AB}}{{BC}}\) (hình vẽ)

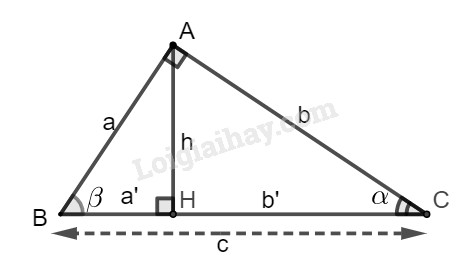
Lời giải chi tiết:

Đặt tên hình như hình dưới đây: 

Xét tam giác vuông \(AHC\):

\(\sin \alpha  = \dfrac{{AH}}{{AC}} = \dfrac{h}{b}.\)

Vậy chọn đáp án (D). 

Bài 2.2

(A) \(cos\alpha  = \dfrac{a}{ b};\)                      (B) \(cos\alpha  =  \dfrac{a}{ c}\);

(C) \(cos\alpha  =  \dfrac{b}{c}\);                      (D) \(cos\alpha  =  \dfrac{b}{{b'}}.\)

Lời giải chi tiết:

Xét tam giác vuông \(ABC\): 

\(\cos \alpha  = \dfrac{{AC}}{{BC}} = \dfrac{b}{c}.\) 

Vậy chọn đáp án (C).

Bài 2.3

(A) \(tg\alpha  = \dfrac{b}{ a}\);                         (B) \(tg\alpha  = \dfrac{b}{c}\) ;

(C) \(tg\alpha  = \dfrac{b}{ h}\);                         (D) \(tg\alpha  = \dfrac{h}{{b'}}\).

Lời giải chi tiết:

Xét tam giác vuông \(AHC\): 

\(tg \alpha  = \dfrac{{AH}}{{HC}} = \dfrac{h}{b'}.\)

Vậy chọn đáp án (D).

Bài 2.4

(A) \(\cot g\alpha  = \dfrac{b}{a}\);                        (B) \(\cot g\alpha  =  \dfrac{b}{c}\);

(C) \(\cot g\alpha  =  \dfrac{a}{c}\);                         (D) \(\cot g\alpha  =  \dfrac{h}{ b}.\)

Lời giải chi tiết:

Xét tam giác vuông \(ABC\):

\(cotg \alpha  = \dfrac{{AC}}{{AB}} = \dfrac{b}{a}.\)

Vậy chọn đáp án (A).

HocTot.Nam.Name.Vn