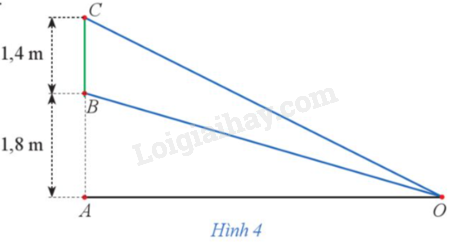
Giải bài 2 trang 35 Chuyên đề học tập Toán 12 - Cánh diềuHình 4 minh hoạ một màn hình (BC) có chiều cao 1,4 m được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng (BA = 1,8)m. Một chiếc đèn quan sát màn hình được đặt ở vị trí (O) trên mặt đất. Hãy tính khoảng cách (AO) sao cho góc quan sát (BOC) là lớn nhất. Đề bài Hình 4 minh hoạ một màn hình \(BC\) có chiều cao 1,4 m được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng \(BA = 1,8\)m. Một chiếc đèn quan sát màn hình được đặt ở vị trí \(O\) trên mặt đất. Hãy tính khoảng cách \(AO\) sao cho góc quan sát \(BOC\) là lớn nhất.
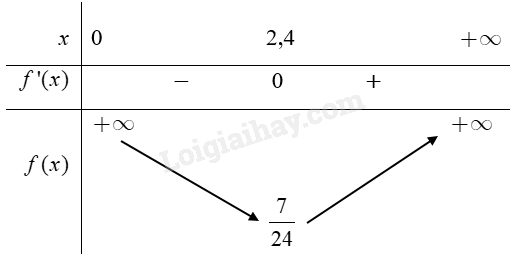
Phương pháp giải - Xem chi tiết +) Do góc \(\widehat {BOC}\)là góc của tam giác nên \({0^0} < \widehat {BOC} < {180^0}\)khi đó \(\widehat {BOC}\)càng lớn thì \(\tan \widehat {BOC}\)cũng càng lớn nên ta sẽ đưa về tìm AO để \(\tan \widehat {BOC}\)lớn nhất. +) Ta cần biểu thị \(\tan \widehat {BOC}\)qua các đoạn thẳng đã và qua AO. Sử dụng công thức: \(\tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\); trong đó \(\widehat {BOC} = \widehat {AOC} - \widehat {AOB}\) +) Ta được \(\tan \widehat {BOC}\)được tính bằng 1 biểu thức chứa \(x\). Khi đó ta xét hàm số tương ứng và tìm giá trị lớn nhất của nó. Lời giải chi tiết Để góc quan sát \(\widehat {BOC}\) lớn nhất thì \(\tan \widehat {BOC}\) là lớn nhất. Giả sử \(AO = x\) (m) \((x > 0).\) Ta có \(\tan \widehat {BOC} = \tan (\widehat {AOC} - \widehat {AOB}) = \frac{{\tan \widehat {AOC} - \tan \widehat {AOB}}}{{1 + \tan \widehat {AOC}.\tan \widehat {AOB}}}\) \(\tan \widehat {BOC} = \frac{{\frac{{AC}}{{AO}} - \frac{{AB}}{{AO}}}}{{1 + \frac{{AC}}{{AO}}.\frac{{AB}}{{AO}}}} = \frac{{\frac{{1,4}}{x}}}{{1 + \frac{{1,8 + 1,4}}{x}.\frac{{1,8}}{x}}} = \frac{{1,4x}}{{{x^2} + 5,76}}.\) Xét hàm số \(f(x) = \frac{{1,4x}}{{{x^2} + 5,76}},\) \(x \in (0; + \infty ).\) Ta có \(f'(x) = \frac{{1,4({x^2} + 5,76) - 1,4x.2x}}{{{{\left( {{x^2} + 5,76} \right)}^2}}} = \frac{{ - 1,4{x^2} + 8,064}}{{{{\left( {{x^2} + 5,76} \right)}^2}}}.\) Do đó \(f'(x) = 0 \Leftrightarrow x = 2,4\) (do \(x > 0\)). Bảng biến thiên của hàm số:
Căn cứ vào bảng biến thiên ta có \(\mathop {\max }\limits_{(0; + \infty )} f(x) = f(2,4) = \frac{7}{{24}}\) tại \(x = 2,4.\) Vậy để góc quan sát \(\widehat {BOC}\) lớn nhất thì khoảng cách \(AO = 2,4\) mét.  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
