Giải bài 5 trang 36 Chuyên đề học tập Toán 12 - Cánh diều

Đề bài

Một nhà máy sản xuất xe đạp cho thị trường châu Âu theo đơn giá 120 euro (€). Chi phí mỗi ngày của nhà máy được cho bởi hàm số

\(K(x) = 0,02{x^3} - 3{x^2} + 172x + 2400.\)

trong đó \(x\) là số lượng xe đạp sản xuất được trong ngày hôm đó. Mỗi ngày có thể sản xuất tối đa 130 xe đạp. Giả sử số xe đạp sản xuất được trong mỗi ngày đề được bán hết vào cuối ngày đó.

Gọi \(G(x)\) là hàm biểu diễn lợi nhuận hằng ngày của nhà máy.

a) Vẽ đồ thị hàm số \(G(x)\) trên đoạn \(\left[ {0;130} \right].\)

b) Số lượng xe mỗi ngày cần sản xuất là bao nhiêu để nhà máy có lãi?

c) Số lượng xe mỗi ngày cần sản xuất là bao nhiêu để nhà máy có lợi nhuận lớn nhất?

d) Giả sử nhà máy quyết định tận dụng tối đa công suất sản xuất 130 xe đạp mỗi ngày. Nhà máy phải chọn đơn giá là bao nhiêu để có lãi?

Lời giải chi tiết

a) Doanh thu một ngày của nhà máy sản xuất là \(P(x) = 120x\) (€), \(x \in {\rm{[0;130]}}\).

Lợi nhuận một ngày của nhà máy là

\(G(x) = P(x) - K(x) = 120x - (0,02{x^3} - 3{x^2} + 172x + 2400)\)

\(G(x) =  - 0,02{x^3} + 3{x^2} - 52x - 2400\) (€),

Vẽ đồ thị hàm số \(G(x)\) trên đoạn \({\rm{[}}0;130]\):

• Ta có \(G'(x) =  - 0,06{x^2} + 6x - 52\)

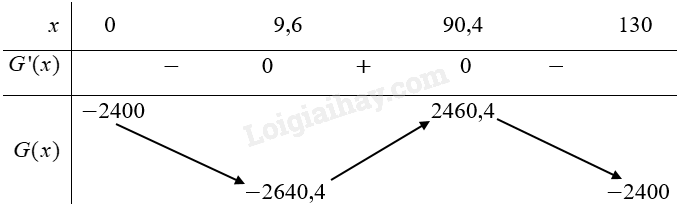
\(G'(x) = 0 \Leftrightarrow x \approx 9,6\) hoặc \(x \approx 90,4.\)

Bảng biến thiên:

Hàm số nghịch biến trên \({\rm{[}}0;9,6)\) và \((90,4;130]\); đồng biến trên khoảng \((9,6;90,4)\).

• Trên đoạn \({\rm{[}}0;130]\) đồ thị hàm số cắt trục hoành tại các điểm \((50;0)\& (120;0)\); đồ thị cắt trục tung tại điểm (0;-2400).
• Vậy ta có đồ thị hàm \(G(x)\) trên đoạn \({\rm{[}}0;130]\) như hình sau:

a) Để nhà máy có lãi thì \(G(x) > 0\).

Từ đồ thị hàm số ở câu a, ta có \(G(x) > 0 \Leftrightarrow x \in (50;120)\).

Mà số lượng xe là số tự nhiên nên \(x \in N\) do đó \(x \in {\rm{[}}51;119]\)

Vậy mỗi ngày phải sản xuất từ 51 dến 119 chiếc xe để có lãi.

b) Từ bảng biến thiên của hàm số \(G(x)\) ở câu a, ta có \(G(x)\) đạt giá trị lớn nhất khi và chỉ khi \(x \approx 90,4\). Vì \(x\) là số tự nhiên nên \(x = 90\) hoặc \(x = 91\) thì lợi nhuận sẽ thu được lớn nhất.

Ta có \(G(90) = 2640\) và \(G(91) = 2639,58\) nên \(G(90) > G(91)\).

Vậy để nhà máy có lợi nhất thì mỗi ngày xần sản xuất 90 chiếc xe máy.

c) Chi phí mỗi ngày của nhà máy khi sản xuất 130 chiếc xe là:

\(K(130) = {0,02.130^3} - {3.130^2} + 172.130 + 2400 = 18000\) (€).

Gọi \(y\)(€) là đơn giá nhà máy bán ra thị trường, khi đó doanh thu nhà máy thu được là \(P(y) = 130y\) (€).

Lợi nhuận nhà máy thu được là \(G(y) = P(y) - K(130) = 130y - 18000\) (€).

Để nhà máy có lãi thì \(G(y) > 0 \Leftrightarrow 130y - 18000 > 0 \Leftrightarrow y > \frac{{1800}}{{13}} \approx 138,46\).

Vậy để nhà máy có lãi thì cần chọn đơn giá lớn hơn 138,46 euro.