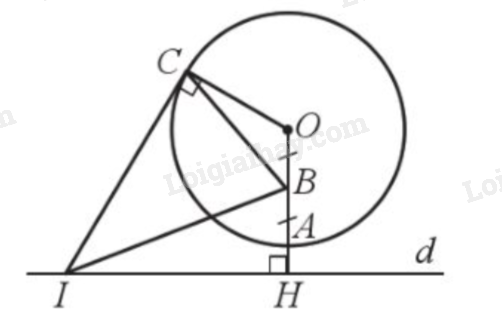
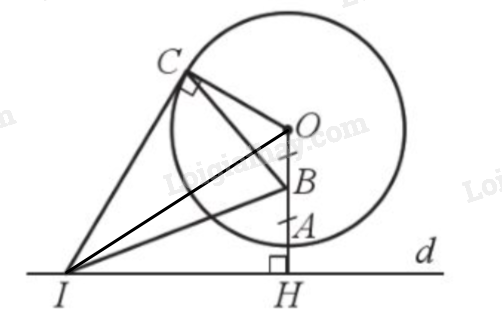
Giải bài 18 trang 107 sách bài tập toán 9 - Cánh diều tập 1Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I. Đề bài Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.
Phương pháp giải - Xem chi tiết Bước 1: Chứng minh \(I{B^2} = I{H^2} + B{H^2} = I{H^2} + 9\). Bước 2: Chứng minh \(I{C^2} = I{O^2} - C{O^2} = O{H^2} + I{H^2} - C{O^2} = I{H^2} + 9\) Lời giải chi tiết
Kẻ OI. Do B trung điểm của OA nên \(OB = BA = \frac{{OA}}{2} = \frac{4}{2} = 2\)cm. Ta có \(HB = OH - OB = 5 - 2 = 3\)cm. Xét tam giác vuông IBH có \(I{B^2} = I{H^2} + B{H^2} = I{H^2} + 9\). Xét tam giác vuông IOC có \(I{C^2} = I{O^2} - C{O^2} = O{H^2} + I{H^2} - C{O^2} = {5^2} + I{H^2} - {4^2} = I{H^2} + 9\) Suy ra \(I{B^2} = I{C^2}\left( { = I{H^2} + 9} \right)\), do đó \(IB = IC\), nên tam giác IBC cân tại B.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
