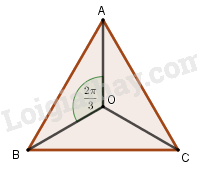
Bài 1.65 trang 40 SBT hình học 11Giải bài 1.65 trang 40 sách bài tập hình học 11. Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc... Đề bài Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc α,0≤α<2π, biến tam giác trên thành chính nó? A. Chỉ có một B. Chỉ có hai C. Chỉ có ba D. Chỉ có bốn Phương pháp giải - Xem chi tiết Dựa vào tính chất của tam giác đều và nhận xét. Lời giải chi tiết
Ta thấy: +) Q(O,0)(A)=A, Q(O,0)(B)=B, Q(O,0)(C)=C nên Q(O,0) biến tam giác ABC thành chính nó. +) Q(O,2π3)(A)=B, Q(O,2π3)(B)=C, Q(O,2π3)(C)=A nên Q(O,2π3) biến tam giác ABC thành tam giác BCA hay chính nó. +) Q(O,4π3)(A)=C, Q(O,4π3)(B)=A, Q(O,4π3)(C)=B nên Q(O,4π3) biến tam giác ABC thành tam giác CAB hay chính nó. Vậy có 3 phép quay cần tìm. Chọn C. HocTot.Nam.Name.Vn
|