Bài 13 trang 104 SBT toán 9 tập 1

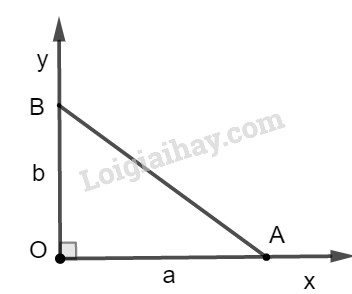
LG a

\(\sqrt {{a^2} + {b^2}}\)        

Phương pháp giải:

Áp dụng định lí Pytago vào tam giác OAB vuông tại O, ta có:

\(A{B^2} = O{A^2} + O{B^2}\)

Lời giải chi tiết:

\(\sqrt {{a^2} + {b^2}}\) 

* Cách dựng:

−  Dựng góc vuông \(xOy\).

−  Trên tia \(Ox\), dựng đoạn \(OA = a\).

−  Trên tia \(Oy\), dựng đoạn \(OB = b\).

−  Nối \(AB\) ta có đoạn \(AB = \sqrt {{a^2} + {b^2}} \) cần dựng.

* Chứng minh:

Áp dụng định lý Pytago vào tam giác vuông \(AOB\), ta có:

\(A{B^2} = O{A^2} + O{B^2}\)\( = {a^2} + {b^2}\) 

Suy ra: \(AB = \sqrt {{a^2} + {b^2}}.\)

LG b

\(\sqrt {{a^2} - {b^2}} \,,\,\left( {a > b} \right)\) 

Phương pháp giải:

Áp dụng định lí Pytago vào tam giác OAB vuông tại O, ta có:

\(A{B^2} = O{A^2} + O{B^2}\)

Lời giải chi tiết:

\(\sqrt {{a^2} - {b^2}} \,,\,\left( {a > b} \right)\) 

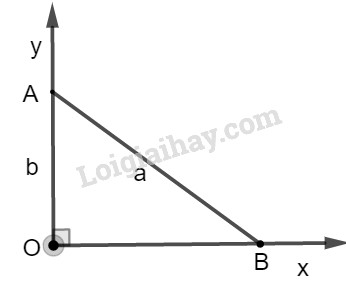
*  Cách dựng :

− Dựng góc vuông \(xOy\).

− Trên tia \(Oy\), dựng đoạn \(OA = b\).

− Dựng cung tròn tâm \(A\), bán kính bằng \(a\) cắt tia \(Ox\) tại \(B\).

Ta có đoạn \(OB = \sqrt {{a^2} - {b^2}} (a > b)\) cần dựng.

*     Chứng minh;

Áp dụng định lí Pytago vào tam giác vuông \(AOB\), ta có:

\(A{B^2} = O{A^2} + O{B^2} \Rightarrow O{B^2} \)\(= A{B^2} - O{A^2} = {a^2} - {b^2}\) 

Suy ra: \(OB = \sqrt {{a^2} - {b^2}} \)

HocTot.Nam.Name.Vn