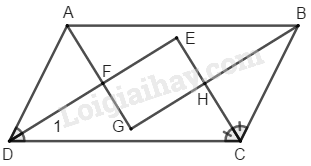
Bài 110 trang 93 SBT toán 8 tập 1

Đề bài

Chứng minh rằng các tia phân giác các góc của một hình bình hành cắt nhau tao thành một hình chữ nhật.

Lời giải chi tiết

Giả sử ABCD là hình bình hành.

Gọi \(G,\, H,\, E, \,K\) lần lượt là giao điểm của các đường phân giác của \(\widehat A\) và \(\widehat B\); \(\widehat B\) và \(\widehat C\); \(\widehat C\) và \(\widehat D\); \(\widehat D\) và \(\widehat A\).

Ta có: \(\widehat {ADF} = \eqalign{1 \over 2}\widehat {ADC}\) (tính chất tia phân giác)

             \(\widehat {DAF} =\eqalign {1 \over 2}\widehat {DAB}\) (tính chất tia phân giác)

            \(\widehat {ADC} + \widehat {DAB} = {180^0}\) (hai góc trong cùng phía)

Suy ra: \(\widehat {ADF} + \widehat {DAF} = \eqalign{1 \over 2}\left( {\widehat {ADC} + \widehat {DAB}} \right)\) \(=\eqalign {1 \over 2}{.180^0} = {90^0}\)

Trong \(∆ AFD\) ta có: 

\(\widehat {AFD} = {180^0} - \left( {\widehat {ADF} + \widehat {DAF}} \right) \) \(= {180^0} - {90^0} = {90^0}\)

\(\widehat {EFG} = \widehat {AFD}\) (đối đỉnh)

\(\eqalign{  &  \Rightarrow \widehat {EFG} = {90^0}  \cr  & \widehat {GAB} = \eqalign{1 \over 2}\widehat {DAB}(gt)  \cr  & \widehat {GBA} = {1 \over 2}\widehat {CBA}(gt) \cr} \)

\(\widehat {DAB} + \widehat {CBA} = {180^0}\) (hai góc trong cùng phía)

\( \Rightarrow \widehat {GBA} + \widehat {GAB}\) \(= \eqalign{1 \over 2}\left( {\widehat {DAB} + \widehat {CBA}} \right)\) \(= \eqalign{1 \over 2}{.180^0} = {90^0}\)

Trong \(∆ AGB\) ta có: \(\widehat {AGB} = {180^0} - \left( {\widehat {GAB} + \widehat {GBA}} \right) \) \(= {180^0} - {90^0} = {90^0}\)

hay \(\widehat G = {90^0}\)

\(\eqalign{  & \widehat {EDC} = \eqalign{1 \over 2}\widehat {ADC}(gt)  \cr  & \widehat {ECD} =\eqalign {1 \over 2}\widehat {BCD}(gt) \cr} \)

\(\widehat {ADC} + \widehat {BCD} = {180^0}\) (hai góc trong cùng phía)

\( \Rightarrow \widehat {EDC} + \widehat {ECD} \) \(= \eqalign{1 \over 2}\left( {\widehat {ADC} + \widehat {BCD}} \right) \) \(= \eqalign{1 \over 2}{.180^0} = {90^0}\)

Trong \(∆ EDC\) ta có: \(\widehat {DEC} = {180^0} - \left( {\widehat {EDC} + \widehat {ECD}} \right)\) \(= {180^0} - {90^0} = {90^0}\) hay \(\widehat E = {90^0}\)

Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).

HocTot.Nam.Name.Vn