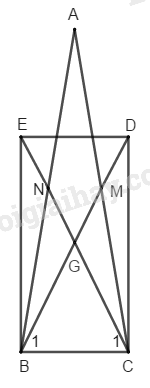
Bài 115 trang 94 SBT toán 8 tập 1

Đề bài

Cho tam giác \(ABC\) cân tại \(A,\) các đường trung tuyến \(BM,\, CN\) cắt nhau tại \(G.\) Gọi \(D\) là điểm đối xứng với \(G\) qua \(M,\) gọi \(E\) là điểm đối xứng với \(G\) qua \(N.\) Tứ giác \(BEDC\) là hình gì ? Vì sao ?

Lời giải chi tiết

* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G

Suy ra: \(G\) là trọng tâm của \(∆ ABC\)

\(⇒ GB = 2GM\) (tính chất đường trung tuyến)

\(GC = 2GN\) (tính chất đường trung tuyến)

Điểm \(D\) đối xứng với điểm \(G\) qua điểm \(M\)

\(⇒ MG = MD\) hay \(GD = 2 GM\)

Suy ra: \(GD = GB\) (1)

Điểm \(E\) đối xứng với điểm \(G\) qua điểm \(N\)

\(⇒ NG = NE\) hay \(GE = 2 GN\)

Suy ra: \(GC = GE\) (2)

Từ (1) và (2) suy ra tứ giác \(BCDE\) là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Xét \(∆ BCM\) và \(∆ CBN:\)

\(BC\) cạnh chung

\(\widehat {BCM} = \widehat {CBN}\) (tính chất tam giác cân ABC)

\(CM = BN\) ( vì \(AB = AC\))

Do đó: \(∆ BCM = ∆ CBN\, (c.g.c)\)

\( \Rightarrow {\widehat B_1} = {\widehat C_1}\) \(⇒ ∆ GBC\) cân tại \(G\) \(⇒ GB = GC ⇒ BD = CE\)

Hình bình hành \(BCDE\) có hai đường chéo bằng nhau nên nó là hình chữ nhật.

HocTot.Nam.Name.Vn