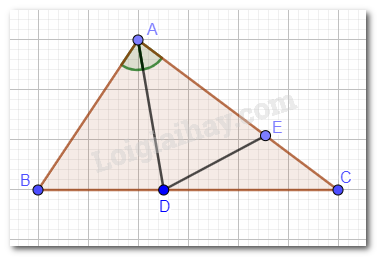
Giải bài 1 trang 86 SGK Toán 7 tập 2 - Cánh diềuChứng minh định lí: “Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn” (trang 74) thông qua việc giải bài tập sua đây: Cho tam giác ABC có AB < AC. Tia phân giác của góc BAC cắt cạnh BC tại D. Điểm E thuộc cạnh AC thỏa mãn AE = AB. Chứng minh: Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Chứng minh định lí: “Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn” (trang 74) thông qua việc giải bài tập sau đây: Cho tam giác ABC có AB < AC. Tia phân giác của góc BAC cắt cạnh BC tại D. Điểm E thuộc cạnh AC thỏa mãn AE = AB. Chứng minh: a) \(\Delta ABD = \Delta AED\); b) \(\widehat B > \widehat C\). Phương pháp giải - Xem chi tiết a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c. b) Chứng minh \(\widehat B > \widehat C\) dựa vào kết quả phần a và tổng ba góc trong một tam giác bằng 180°. Lời giải chi tiết
a) Xét hai tam giác ABD và AED: AB = AE, AD chung, \(\widehat {BAD} = \widehat {EAD}\)(AD là phân giác của góc BAC). Vậy \(\Delta ABD = \Delta AED\) (c.g.c) b) Ta có: \(\Delta ABD = \Delta AED \) suy ra \(\widehat {ABD} = \widehat {AED}\) (2 góc tương ứng) Ba điểm A, E, C thẳng hàng nên \(\widehat {AEC} = 180^\circ \). Vậy \(\widehat {ABD} = \widehat {AED} = 180^\circ - \widehat {DEC} = \widehat {EDC} + \widehat {ECD}\)(Tổng ba góc trong tam giác EDC bằng 180°). Do đó, góc B bằng tổng của góc EDC và góc C. Vậy \(\widehat B > \widehat C\).
|