Đề thi học kì 2 Toán 6 - Đề số 13 - Cánh diềuTổng hợp đề thi học kì 2 lớp 6 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài
I. Trắc nghiệm
Câu 1 :
Cách viết nào sau đây không phải phân số?
Câu 2 :
Số đối của phân số \(\frac{{ - 15}}{{16}}\) là
Câu 3 :
Số nguyên \(x\) thỏa mãn điều kiện \(\frac{x}{3} = \frac{6}{{ - 9}}\) là
Câu 4 :
Tỉ số phần trăm của 16 và 20 là
Câu 5 :
Nam mua một quyển sách có giá bìa là 50000 đồng. Khi trả tiền được cửa hàng giảm giá \(10\% \). Hỏi Nam mua quyển sách đó hết bao nhiêu tiền?
Câu 6 :
Làm tròn số 131,2956 đến hàng phần trăm được kết quả là
Câu 7 :
Biết \(\frac{3}{5}\) của một số bằng (-30), số đó là
Câu 8 :
Đổi hỗn số \( - 3\frac{2}{5}\) ra phân số, kết quả là:
Câu 11 :
Trên đường thẳng a lấy 10 điểm phân biệt. Số đoạn thẳng trong hình vẽ là:
Câu 12 :
Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là:
II. Tự luận
Câu 1 :
1) Thực hiện phép tính: a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\) b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\) 2) Tìm \(x\) biết: a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\) b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\)
Câu 2 :
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại. a) Tính số học sinh mỗi loại của lớp? b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
Câu 3 :
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại. a) Tính số học sinh mỗi loại của lớp? b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
Câu 4 :
Cho hai tia \({\rm{Ox}},{\rm{Oy}}\) đối nhau. Trên tia \({\rm{Ox}}\) lấy điểm \({\rm{A}}\) sao cho \({\rm{OA}} = 4\;{\rm{cm}}\). Trên tia \({\rm{Oy}}\) lấy điểm \({\rm{B}}\) sao cho \({\rm{OB}} = 2\;{\rm{cm}}\). Gọi \({\rm{C}}\) là trung điểm của đoạn thẳng \({\rm{OA}}\). a) Tính độ dài đoạn thẳng \({\rm{AB}}\). b) Điểm \({\rm{O}}\) có là trung điểm của đoạn thẳng \({\rm{BC}}\) không? Vì sao? c) Vẽ tia \({\rm{Oz}}\) khác các tia \({\rm{Ox}},{\rm{Oy}}\). Viết tên các góc có trong hình vẽ.
Câu 5 :
So sánh S với 2, biết \(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\). Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Cách viết nào sau đây không phải phân số?
Đáp án : C Phương pháp giải :
Phân số có dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\). Lời giải chi tiết :
\(\frac{{2,5}}{3}\) không phải là phân số vì \(2,5 \notin \mathbb{Z}\). Đáp án C.
Câu 2 :
Số đối của phân số \(\frac{{ - 15}}{{16}}\) là
Đáp án : B Phương pháp giải :
Hai phân số được gọi là đối nhau nếu tổng của chúng bằng 0. Lời giải chi tiết :
Vì \(\frac{{ - 15}}{{16}} + \frac{{15}}{{16}} = 0\) nên \(\frac{{15}}{{16}}\) là số đối của phân số \(\frac{{ - 15}}{{16}}\). Đáp án B.
Câu 3 :
Số nguyên \(x\) thỏa mãn điều kiện \(\frac{x}{3} = \frac{6}{{ - 9}}\) là
Đáp án : B Phương pháp giải :
Hai phân số \(\frac{a}{b} = \frac{c}{d}\left( {b,d \ne 0} \right)\) nếu \(a.d = c.b\) Lời giải chi tiết :
\(\begin{array}{l}\frac{x}{3} = \frac{6}{{ - 9}}\\x.\left( { - 9} \right) = 6.3\\ - 9x = 18\\x = - 2\end{array}\) Đáp án B.
Câu 4 :
Tỉ số phần trăm của 16 và 20 là
Đáp án : D Phương pháp giải :
Tỉ số phần trăm của a và b là \(\frac{a}{b}.100\% \). Lời giải chi tiết :
Tỉ số phần trăm của 16 và 20 là \(\frac{{16}}{{20}}.100 = 0,8.100\% = 80\% \). Đáp án D.
Câu 5 :
Nam mua một quyển sách có giá bìa là 50000 đồng. Khi trả tiền được cửa hàng giảm giá \(10\% \). Hỏi Nam mua quyển sách đó hết bao nhiêu tiền?
Đáp án : D Phương pháp giải :
m% của a là \(m\% .a\). Lời giải chi tiết :
Vì cửa hàng giảm giá 10% nên số tiền Nam trả ứng với: 100% - 10% = 90%. Vậy Nam mua quyển sách đó hết: \(90\% .50000 = 45000\) (đồng) Đáp án D.
Câu 6 :
Làm tròn số 131,2956 đến hàng phần trăm được kết quả là
Đáp án : A Phương pháp giải :
Dựa vào kiến thức làm tròn số. Lời giải chi tiết :
Số 131,2956 làm tròn đến hàng phần trăm ta được 131,30. Đáp án A.
Câu 7 :
Biết \(\frac{3}{5}\) của một số bằng (-30), số đó là
Đáp án : C Phương pháp giải :
Biết \(\frac{m}{n}\) của a là b, ta tính được \(a = b:\frac{m}{n}\) Lời giải chi tiết :
Số cần tìm là: \( - 30:\frac{3}{5} = - 50\). Đáp án C.
Câu 8 :
Đổi hỗn số \( - 3\frac{2}{5}\) ra phân số, kết quả là:
Đáp án : A Phương pháp giải :
Sử dụng quy tắc đổi hỗn số thành phân số. Lời giải chi tiết :
Ta có: \( - 3\frac{2}{5} = - \frac{{3.5 + 2}}{5} = - \frac{{17}}{5}\). Đáp án A.
Đáp án : B Phương pháp giải :
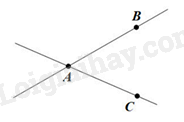
Quan sát hình vẽ để trả lời. Lời giải chi tiết :
Hình vẽ trên là hai đường thẳng AB và AC cắt nhau tại A, chỉ có 1 điểm chung nên ta chọn đáp án B. Đáp án B.
Đáp án : B Phương pháp giải :
Quan sát hình vẽ để trả lời câu hỏi. Lời giải chi tiết :
Hai tia đối nhau phải là hai tia có chung gốc nên đáp án A, B, D sai. Chỉ có Bx và By đúng. Đáp án B.
Câu 11 :
Trên đường thẳng a lấy 10 điểm phân biệt. Số đoạn thẳng trong hình vẽ là:
Đáp án : C Phương pháp giải :
Đếm số đoạn thẳng Lời giải chi tiết :
Số đoạn thẳng là 45. Đáp án C.
Câu 12 :
Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là:
Đáp án : A Phương pháp giải :
Vẽ hình mô tả để xác định Lời giải chi tiết :
Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là: góc nhọn. Đáp án A.
II. Tự luận
Câu 1 :
1) Thực hiện phép tính: a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\) b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\) 2) Tìm \(x\) biết: a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\) b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\) Phương pháp giải :
Áp dụng quy tắc cộng, trừ, nhân, chia. Lời giải chi tiết :
1) a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\)\( = \frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - \frac{1}{2}} \right)\)\( = \frac{1}{4} + \frac{3}{4} \cdot \frac{1}{6}\)\( = \frac{1}{4} + \frac{1}{8}\)\( = \frac{3}{8}\) b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\)\( = \left( {1\frac{3}{{25}} - \frac{3}{{25}}} \right) + \left( {\frac{{ - 17}}{{19}} + \frac{{ - 2}}{{19}}} \right) + \frac{{2022}}{{2023}}\) \( = 1 + ( - 1) + \frac{{2022}}{{2023}}\) \( = \frac{{2022}}{{2023}}.\) 2) a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\) \(\frac{2}{3}x = \frac{1}{{10}} + \frac{1}{2}\) \(\frac{2}{3}x = \frac{3}{5}\) \(x = \frac{3}{5}:\frac{2}{3}\) \(x = \frac{3}{5}:\frac{2}{3}\) \(x = \frac{9}{{10}}\) Vậy \(x = \frac{9}{{10}}\). b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\) \(5,16 - 2x = - 2,4\) \(2x = 5,16 - ( - 2,4)\) \(2x = 7,56\) \(x = 7,56:2\) \(x = 3,78\) Vậy \(x = 3,78\)
Câu 2 :
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại. a) Tính số học sinh mỗi loại của lớp? b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp? Phương pháp giải :
a) Tính \(\frac{m}{n}\) của a bằng \(\frac{m}{n}.a\). b) Số phần trăm của a với b là \(\frac{{a.100}}{b}\% \) Lời giải chi tiết :
a) Số học sinh xếp loại tốt là: \(40 \cdot \frac{2}{5} = 16\) ( học sinh) Số học sinh xếp loại khá là: \((40 - 16) \cdot \frac{5}{8} = 15\) (học sinh) Số học sinh xếp loại đạt là: \(40 - 16 - 15 = 9\) (học sinh) b) Số học sinh xếp loại đạt chiếm số phần trảm của lớp là: \(\frac{{9.100}}{{40}}\% = 22,5\% \)
Câu 3 :
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại. a) Tính số học sinh mỗi loại của lớp? b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp? Phương pháp giải :
a) Tính \(\frac{m}{n}\) của a bằng \(\frac{m}{n}.a\). b) Số phần trăm của a với b là \(\frac{{a.100}}{b}\% \) Lời giải chi tiết :
a) Số học sinh xếp loại tốt là: \(40 \cdot \frac{2}{5} = 16\) ( học sinh) Số học sinh xếp loại khá là: \((40 - 16) \cdot \frac{5}{8} = 15\) (học sinh) Số học sinh xếp loại đạt là: \(40 - 16 - 15 = 9\) (học sinh) b) Số học sinh xếp loại đạt chiếm số phần trảm của lớp là: \(\frac{{9.100}}{{40}}\% = 22,5\% \)
Câu 4 :
Cho hai tia \({\rm{Ox}},{\rm{Oy}}\) đối nhau. Trên tia \({\rm{Ox}}\) lấy điểm \({\rm{A}}\) sao cho \({\rm{OA}} = 4\;{\rm{cm}}\). Trên tia \({\rm{Oy}}\) lấy điểm \({\rm{B}}\) sao cho \({\rm{OB}} = 2\;{\rm{cm}}\). Gọi \({\rm{C}}\) là trung điểm của đoạn thẳng \({\rm{OA}}\). a) Tính độ dài đoạn thẳng \({\rm{AB}}\). b) Điểm \({\rm{O}}\) có là trung điểm của đoạn thẳng \({\rm{BC}}\) không? Vì sao? c) Vẽ tia \({\rm{Oz}}\) khác các tia \({\rm{Ox}},{\rm{Oy}}\). Viết tên các góc có trong hình vẽ. Phương pháp giải :
Vẽ hình theo hướng dẫn. a) Xác định độ dài đoạn thẳng AB qua OA và OB. b) Chứng minh OB = OC và O nằm giữa B và C nên O là trung điểm của BC. c) Vẽ tia Oz và kể tên các góc trong hình. Lời giải chi tiết :
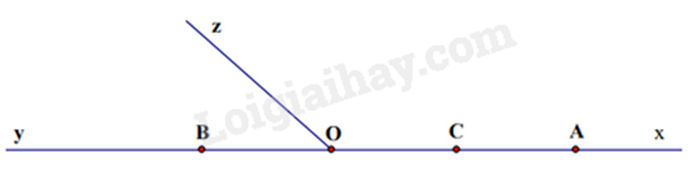
Vẽ hình
a) Theo hình vẽ: \(AB = OA + OB = 4 + 2 = 6\;{\rm{cm}}\) Vậy \(AB = 6\;{\rm{cm}}\) b) Vì C là trung điểm của đoạn thẳng \({\rm{OA}}\) nên \(OC = \frac{{OA}}{2} = \frac{4}{2} = 2\;{\rm{cm}}\) Suy ra \({\rm{OB}} = {\rm{OC}}\) Lại có \({\rm{O}}\) nằm giữa \({\rm{B}}\) và \({\rm{C}}\) Do đó O là trung điểm của đoạn thẳng \({\rm{BC}}\) Vậy \({\rm{O}}\) là trung điểm của đoạn thẳng \({\rm{BC}}\). c)
Các góc có trong hình vẽ là: \(\widehat {{\rm{xOz}}};\widehat {{\rm{yOz}}};\widehat {{\rm{xOy}}},\widehat {xAy},\widehat {xCy},\widehat {xBy}\)
Câu 5 :
So sánh S với 2, biết \(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\). Phương pháp giải :
Nhân hai vế của S với 2 để rút gọn S. Lời giải chi tiết :
\(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\) \(2S = 1 + \frac{2}{2} + \frac{3}{{{2^2}}} + \frac{4}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2022}}}}\) \(2S - S = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2022}}}} - \frac{{2023}}{{{2^{2023}}}}\) \(S = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2022}}}} - \frac{{2023}}{{{2^{2023}}}}\) \(2S = 2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2021}}}} - \frac{{2023}}{{{2^{2022}}}}\) \(2S - S = 2 - \frac{{2024}}{{{2^{2022}}}} + \frac{{2023}}{{{2^{2023}}}}\) \(S = 2 - \frac{{4048 - 2023}}{{{2^{2023}}}}\) Vậy \(S < 2\).
|
