Đề thi giữa kì 2 Toán 6 - Đề số 1 - Cánh diềuTải vềPhần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Giá trị của x trong biểu thức \(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\) là: A. -8 B. -2 C. 8 D. 2 Câu 2: Hình bên có mấy tia:
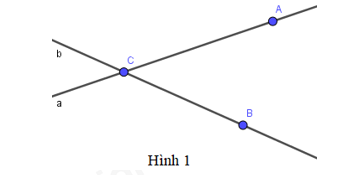
A. 6 B. 3 C. 4 D. 8 Câu 3: Để điều tra về loài hoa yêu thích nhất của \(30\) học sinh lớp 6A1, bạn lớp trưởng thu được bảng dữ liệu như sau:
Viết tắt: H: Hoa Hồng; M: Hoa Mai; C: Hoa Cúc; Đ: Hoa Đào; L: Hoa Lan. Bảng dữ liệu trên điều tra về A. xếp loại học lực của 30 học sinh lớp 6A1. B. loài hoa yêu thích của 30 học sinh lớp 6A1. C. số lượng học sinh lớp 6A1. D. loài hoa trồng được của 30 học sinh lớp 6A1 Câu 4: Chọn phát biểu sai trong các phát biểu sau: A. Điểm A thuộc đường thẳng a B. Hai điểm A, B cùng thuộc đường thẳng a C. Điểm C thuộc đường thẳng b D. Hai điểm B, C cùng thuộc đường thẳng b Phần II. Tự luận (8 điểm): Bài 1: (2 điểm) Thực hiện phép tính (tính hợp lý nếu có thể): a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\) b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\) c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\) Bài 2: (1,5 điểm) Tìm x, biết: a) \(x - \dfrac{{ - 1}}{5} = 1\dfrac{1}{2}\) b) \( - \dfrac{1}{2} + \left( {x - \dfrac{5}{{11}}} \right) = \dfrac{{ - 3}}{4}\) c) \(\dfrac{3}{4} + \left( {\dfrac{2}{5} - x} \right) = \dfrac{1}{4}\) Bài 3: (1,5 điểm) Biểu đồ trang dưới đây cho biết số lượng sách giáo khoa lớp 6 – Bộ Chân trời sáng tạo, bán được tại một hiệu sách vào ngày Chủ nhật vừa qua. a) Sách nào bán được nhiều nhất? Tính số lượng? b) Tổng số cuốn sách giáo khoa lớp 6 mà hiệu sách bán được trong ngày Chủ nhật vừa qua là bao nhiêu cuốn? Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm. a) Tính độ dài đoạn thẳng KQ. b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK. Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao? c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ? Bài 5: (0,5 điểm) Tính giá trị của biểu thức: \(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\) Lời giải Phần I: Trắc nghiệm
Câu 1 Phương pháp: Đưa về hai phân số cùng mẫu và so sánh hai phân số bằng nhau hoặc nhân chéo. Cách giải: Cách 1: \(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\) \(\begin{array}{l}\dfrac{{3x}}{{12}} = \dfrac{{ - 6}}{{12}}\\3x = - 6\\x = - 2\end{array}\) Cách 2: \(\begin{array}{l}\dfrac{x}{4} = \dfrac{6}{{ - 12}}\\x = \dfrac{{4.6}}{{ - 12}}\\x = - 2\end{array}\) Chọn B. Câu 2 Phương pháp: Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O. Cách giải: Hình trên có 6 tia: Ax, Ay, Bx, By, Cx, Cy. Chọn A. Câu 3 Phương pháp: Sử dụng lý thuyết bảng dữ liệu ban đầu. Cách giải: Bảng dữ liệu trên điều tra về loài hoa yêu thích của 30 học sinh lớp 6A1. Chọn B. Câu 4 Phương pháp: Quan sát hình vẽ để xác định một điểm thuộc hay không thuộc một đường thẳng. Từ hình vẽ ta thấy điểm A, C thuộc đường thẳng a; điểm B, C thuộc đường thẳng b. Vậy phát biểu sai là hai điểm A, B cùng thuộc đường thẳng a. Chọn B. Phần II: Tự luận Bài 1 Phương pháp a) Cộng hai phân số cùng mẫu. b) Nhóm thích hợp các phân số cùng mẫu. c) Sử dụng tính chất phân phối của phép nhân và phép cộng. Cách giải: a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\) \(\begin{array}{l} = \dfrac{{ - 7 + 3}}{{16}}\\ = \dfrac{{ - 4}}{{16}}\\ = \dfrac{{ - 1}}{4}\end{array}\) b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\) \(\begin{array}{l} = \left( {\dfrac{1}{7} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}} \right) + \dfrac{{ - 1}}{3}\\ = \dfrac{{1 + 10 - 4}}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{7}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{3}{3} + \dfrac{{ - 1}}{3}\\ = \dfrac{{3 - 1}}{3}\\ = \dfrac{2}{3}\end{array}\) c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\) \(\begin{array}{l} = \dfrac{4}{9}.\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{ - 45}}{{26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}.\dfrac{{ - 7 - 45}}{{26}} + \dfrac{1}{3}\\ = \dfrac{4}{9}.\left( { - 2} \right) + \dfrac{1}{3}\\ = \dfrac{{ - 8}}{9} + \dfrac{3}{9}\\ = \dfrac{{ - 8 + 3}}{9}\\ = \dfrac{{ - 5}}{9}\end{array}\) Bài 2 Phương pháp Chuyển vế để tìm được \(x\). Sử dụng phép tính giá trị lũy thừa của một số. Cách giải Áp dụng quy tắc chuyến vế và đổi dấu để tìm x. Cách giải:
Bài 3 Phương pháp Đọc dữ liệu ở biểu đồ tranh, thực hiện phép tính nhân Cách giải: a) Sách Toán có \(7\) hình Sách Tin học, sách Lịch sử và Địa lí có \(2\) hình b) Tổng số có \(21\) hình Bài 4 Phương pháp a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ. b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK. Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK. c) Tính BA. Chứng minh A nằm giữa B và K. Tính BK = BA + AK. So sánh BK và AQ. Cách giải:
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q. => AK + KQ = AQ => 3 + KQ = 4 => KQ = 4 – 3 => KQ = 1 (cm) b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K. => CK = AC + AK => CK = 3 + 3 => CK = 6 (cm) Ta có: A nằm giữa C và K. AC = AK = 3cm. => A là trung điểm của CK. c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm). Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K. => BK = BA + AK => BK = 1,5 + 3 => BK = 4,5 (cm) Mà AQ = 4 (cm) => BK > AQ. Bài 5 Phương pháp Nhận xét: \(\dfrac{1}{{1.2}} = 1 - \dfrac{1}{2};\) \(\dfrac{1}{{2.3}} = \dfrac{1}{2} - \dfrac{1}{3};\)\(\dfrac{1}{{3.4}} = \dfrac{1}{3} - \dfrac{1}{4};\)…; \(\dfrac{1}{{2011.2012}} = \dfrac{1}{{2011}} - \dfrac{1}{{2012}}\) sau đó rút gọn các cặp phân số đối nhau rồi thực hiện tính. Cách giải: \(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\) \( = 7.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \ldots + \dfrac{1}{{2011.2012}}} \right)\) \( = 7.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots + \dfrac{1}{{2011}} - \dfrac{1}{{2012}}} \right)\) \( = 7.\left( {1 - \dfrac{1}{{2012}}} \right) = \dfrac{{14077}}{{2012}}\)
|













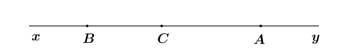
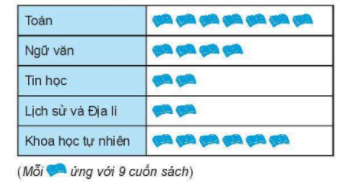
 nên bán được nhiều nhất và số sách Toán bán được là \(7.9 = 63\) (cuốn sách)
nên bán được nhiều nhất và số sách Toán bán được là \(7.9 = 63\) (cuốn sách)
