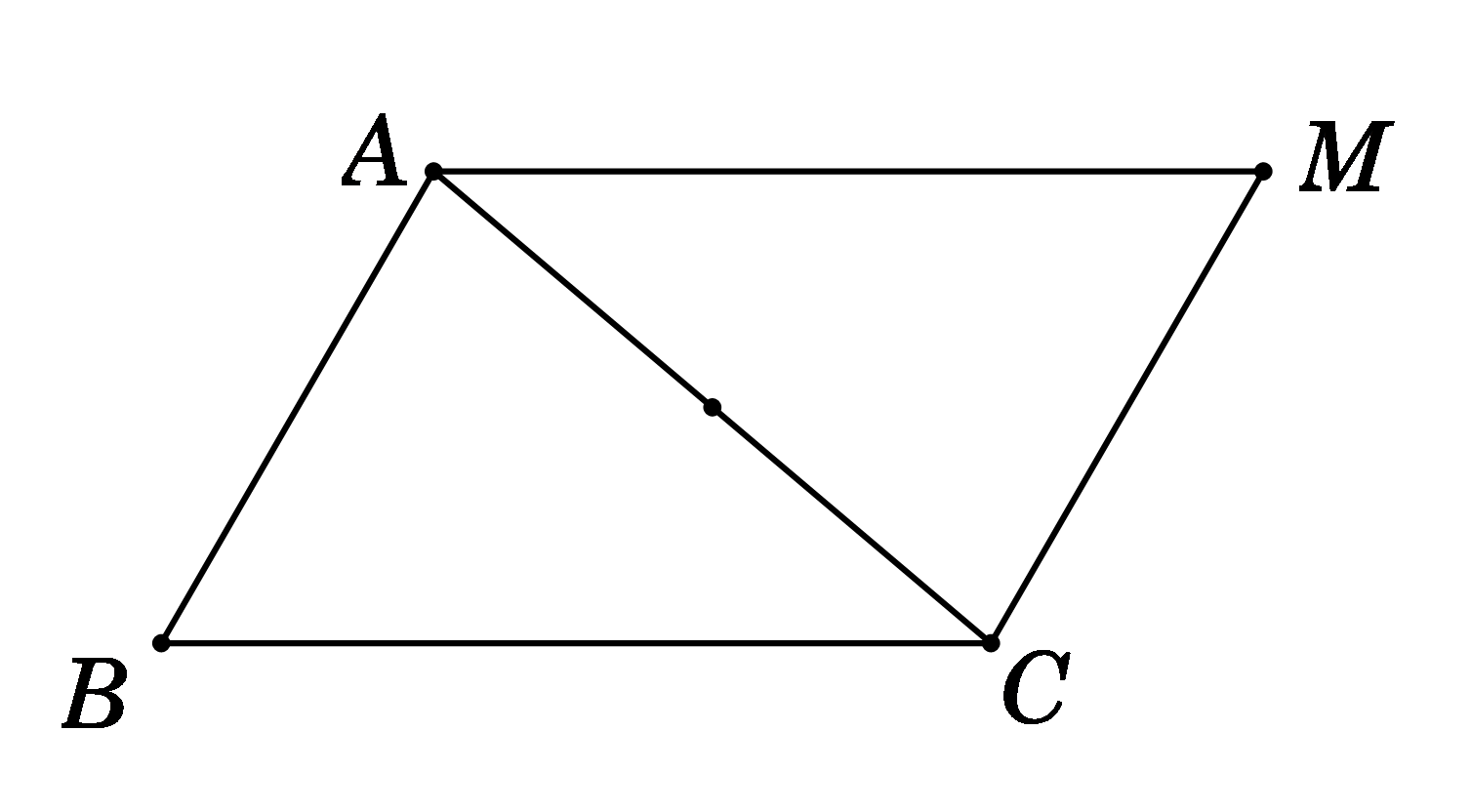Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 4Tải về Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam. c) (5 + 7 + 4 = 15) d) Năm 2018 là năm nhuận. Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
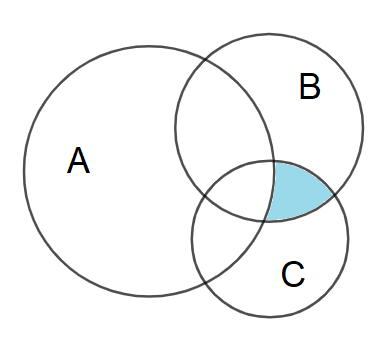
Đề bài Phần 1: Trắc nghiệm (30 câu – 6 điểm) Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam. c) \(5 + 7 + 4 = 15\) d) Năm 2018 là năm nhuận. A. 1 B. 2 C. 3 D. 4 Câu 2: Cho số gần đúng a = 23748023 với độ chính xác d = 123. Hãy viết số quy tròn của số a. A. 23749000. B. 23748000. C. 23746000. D. 23737000. Câu 3: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai? A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \) C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \) Câu 4: Cho tam giác ABC có \(AB = \sqrt 5 ,{\mkern 1mu} {\mkern 1mu} AC = \sqrt 2 \) và \(\angle C = {45^0}\). Tính độ dài cạnh BC. A. \(3\) B. \(2\) C. \(\sqrt 3 \) D. \(\sqrt 2 \) Câu 5: Cặp số (x;y) nào là sau đây là một nghiệm của bất phương trình \(x--2y + 5 > 0\). A. (x;y) = (0;4). B. (x;y) = (2;5). C. (x;y) = (2;3). D. (x;y) = (1;4). Câu 6: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai? A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \) C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \) Câu 7: Tam giác ABC có \(\angle A = {45^0},{\mkern 1mu} {\mkern 1mu} c = 6,{\mkern 1mu} {\mkern 1mu} \angle B = {75^0}\). Độ dài bán kính đường tròn ngoại tiếp tam giác bằng: A. \(8\sqrt 3 \) B. \(2\sqrt 3 \) C. \(6\sqrt 3 \) D. \(4\sqrt 3 \) Câu 8: Cho tam giác ABC với ba cạnh a, b, c. Khi đó \(\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}\) bằng A. \(\frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}\) B. \(\frac{{{a^2} + {b^2} + {c^2}}}{{abc}}\) C. \(\frac{{2\left( {{a^2} + {b^2} + {c^2}} \right)}}{{abc}}\) D. \(\frac{{{a^2} + {b^2} + {c^2}}}{{4abc}}\) Câu 9: Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}|{x^2} - 7x + 6 = 0} \right\}\)và \(B = \left\{ {x \in \mathbb{R}|\left| x \right| > 4} \right\}\). Khẳng định nào sau đây đúng? A. \(A \cup B = A\) B. \(A \cap B = A \cup B\) C. \(\left( {A\backslash B} \right) \subset A\) D. \(B\backslash A = \emptyset \) Câu 10: Cho các tập hợp A, B, C được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
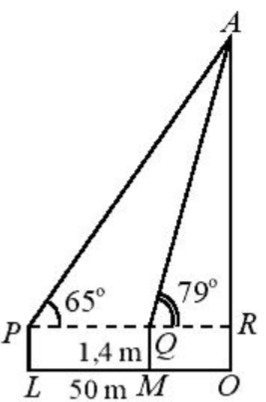
A. \(A \cap B \cap C.\) B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right).\) C. \(\left( {B \cup C} \right)\backslash A.\) D. \(\left( {B \cap C} \right)\backslash A.\) Câu 11: Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh toà nhà với góc nâng \(\angle RQA = {79^0}\), người đó lùi ra xa một khoảng cách LM = 50 m thì nhìn thấy đỉnh toà nhà với góc nâng \(\angle RPA = {65^0}\). Hãy tính chiều cao của toà nhà (làm tròn đến chữ số thập phân thứ nhất), biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4m.
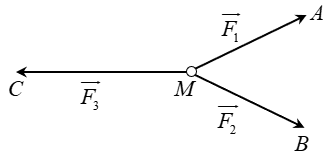
A. 135,8m B. 183,5m C. 158,3m D. 185,3m Câu 12: Biết \(\sin x = \frac{1}{{\sqrt 3 }}\). Giá trị của biểu thức \(P = 2{\sin ^2}x - {\cos ^2}x\) là A. \( - \frac{4}{3}\) B. \(0\) C. \(\frac{4}{3}\) D. \(\frac{2}{3}\) Câu 13: Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}|\left( {2{x^2} - 7x + 5} \right)\left( {x - 2} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{Z}| - 3 < 2x + 1 < 5} \right\}\) Kết luận nào sau đây là đúng? A. \(A \cap B = \left\{ { - 1;{\mkern 1mu} {\mkern 1mu} \frac{5}{2};{\mkern 1mu} {\mkern 1mu} 2} \right\}\) B. \(A \cap B = \left\{ 1 \right\}\) C. \(A \cap B = \left\{ { - 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} \frac{5}{2};{\mkern 1mu} {\mkern 1mu} 2} \right\}\) D. \(A \cap B = \left\{ { - 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\) Câu 14: Cho \(\cos \alpha {\rm{ \;}} = \frac{1}{4}\). Giá trị của \(P = \frac{{\tan \alpha {\rm{ \;}} + 2\cot \alpha }}{{2\tan \alpha {\rm{ \;}} + 3\cot \alpha }}\) là: A. \( - \frac{{17}}{{33}}\) B. \(\frac{{17}}{{33}}\) C. \(\frac{1}{2}\) D. \(\frac{{16}}{{33}}\) Câu 15: Cho ba lực \(\overrightarrow {{F_1}} {\rm{ \;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{ \;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{ \;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 50N và góc \(\widehat {AMB} = {60^\circ }\). Khi đó cường độ lực \(\overrightarrow {{F_1}} \) của là
A. \(100\sqrt 3 N\) B. \(25\sqrt 3 N\) C. \(50\sqrt 3 N\) D. \(50\sqrt 2 N\) Câu 16: Cho ba véctơ bất kì \(\vec u,\vec v,\vec w\) bất kì. Mệnh đề nào sau đây đúng? A. \(\left| {\vec u + \vec v + \vec w} \right| \ge \left| {\vec u} \right| + \left| {\vec v} \right| + \left| {\vec w} \right|\) B. \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| + \left| {\vec v} \right|\) C. \(\left| {\vec u + \vec v + \vec w} \right| \ge \left| {\vec u} \right| - \left| {\vec v} \right| + \left| {\vec w} \right|\) D. \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| - \left| {\vec v} \right|\) Câu 17: Người ta chọn một số bút bi của hai hãng sản xuất A và B thử xem sử dụng một bút thì sau bao nhiêu giờ thì hết mực. Kết quả như sau (đơn vị giờ): Loại bút A: \(\begin{array}{*{20}{c}}{23}&{25}&{27}&{28}&{30}&{35}\end{array}\) Loại bút B: \(\begin{array}{*{20}{c}}{16}&{22}&{28}&{33}&{46}\end{array}\) Nhận xét nào sau đây là đúng? A. Loại bút A có thời gian sử dụng lâu hơn và chất lượng của loại bút A không đồng đều. B. Loại bút A có thời gian sử dụng lâu hơn và chất lượng của loại bút A đồng đều. C. Loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B không đồng đều. D. Loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B đồng đều. Câu 18: Phương sai của một mẫu số liệu \(\left\{ {{x_1};{x_2};...;{x_N}} \right\}\) bằng A. Hai lần độ lệch chuẩn. B. Căn bậc hai của độ lệch chuẩn. C. \(\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^2}} .\) D. Bình phương của độ lệch chuẩn. Câu 19: Cho tam giác ABC vuông cân tại A có AB = 6. Giá trị của \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng A. 0. B. 36. C. -36. D. \(36\sqrt 2 .\) Câu 20: Quan sát 9 con chuột chạy quanh một căn phòng và ghi lại thời gian (tính bằng phút) của chúng trong bảng sau:
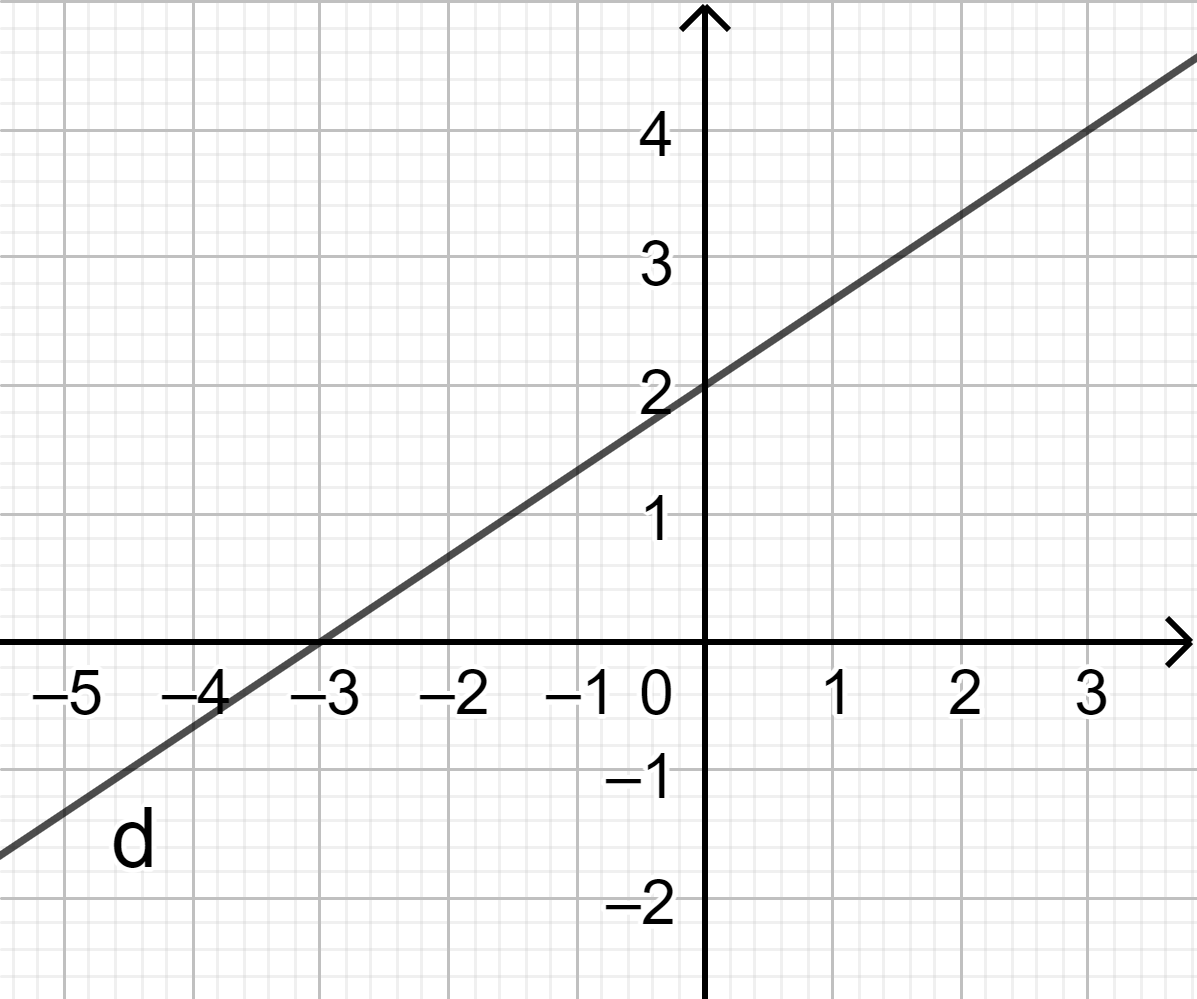
Số trung vị và Mốt của mẫu số liệu thống kê trên lần lượt là A. 5 và 9 B. 2 và 30 C. 1,5 và 1 D. 1,5 và 2 Câu 21: (ID: 590911) Đường thẳng \(2x - 3y + 6 = 0\) chia mặt phẳng tọa độ thành các miền như hình vẽ. Miền nghiệm của \(2x - 3y + 6 \ge 0\) là:
A. Nửa mặt phẳng bờ d chứa gốc tọa độ O và có lấy đường thẳng d. B. Nửa mặt phẳng bờ d chứa gốc tọa độ O và có lấy đường thẳng d. C. Nửa mặt phẳng bờ d không chứa gốc tọa độ O và không lấy đường thẳng d. D. Nửa mặt phẳng bờ d không chứa gốc tọa độ O và không lấy đường thẳng d. Câu 22: Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > - 3}\\{3x - y < 5}\\{y - 1 > 0}\end{array}} \right.\). A. \(\left( { - 2; - 1} \right)\) B. \(\left( {2;0} \right)\) C. \(\left( {3;2} \right)\) D. \(\left( {0,2} \right)\) Câu 23: Giá trị của biểu thức \(B = \cos {0^0} + \cos {20^0} + \cos {40^0} + ... + \cos {160^0} + \cos {180^0}\) là A. \(0\) B. \(1\) C. \( - 1\) D. \(\frac{1}{2}\) Câu 24: Cho tam giác đều ABC có độ dài các cạnh bằng 6 và điểm M thỏa mãn \(\overrightarrow {BM} {\rm{ \;}} = {\rm{ \;}} - \frac{1}{3}\overrightarrow {BC} \). Tích vô hướng \(\overrightarrow {BM} .\overrightarrow {BA} \) bằng A. \(6\) B. \( - 6\sqrt 3 .\) C. \(6\sqrt 3 .\) D. \( - 6.\) Câu 25: Độ dài của cầu Bến Thủy 2 (Nghệ An) người ta đo được là \(996m \pm 0,5m\), có nghĩa là: A. Độ dài đúng của cầu là một số nằm trong khoảng 995,5m đến 996,5m. B. Độ dài đúng của cầu là một số lớn hơn 996m. C. Độ dài đúng của cầu là một số nhỏ hơn 996m. D. Độ dài đúng của cầu là 995,5m hoặc là 996,5m. Câu 26: Hình chữ nhật có các cạnh \(x = 2m \pm 1cm,\,\,y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số tương đối của giá trị đó là: A. 10m2 và 0,5 % B. 10m2 và 0,4 % C. 10m2 và 0,9 % D. 10m2 và 2% Câu 27: Khoảng biến thiên của mẫu số liệu 13; 16; 9; 10; 5; 8; 11; 17; 6; 20 là: A. 5. B. 8. C. 15. D. 20. Câu 28: Trong đợt hội diễn văn nghệ chào mừng 20/11, lớp 10A đăng kí hai tiết mục là múa và diễn kịch. Trong danh sách, có 9 học sinh tham gia tiết mục múa, 13 học sinh tham gia diễn kịch; trong đó có 4 học sinh tham gia cả tiết mục múa và diễn kịch. Hỏi lớp 10A có tất cả bao nhiêu học sinh tham gia hội diễn văn nghệ? A. 15. B. 18. C. 21. D. 26. Câu 29: Cho hình vuông ABCD có cạnh bằng \(a\). Khi đó \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right|\) bằng: A. \(\frac{{a\sqrt 5 }}{2}\) B. \(\frac{{a\sqrt 3 }}{2}\) C. \(\frac{{a\sqrt 3 }}{3}\) D. \(a\sqrt 5 \) Câu 30: Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) khi \(2\vec a.\vec b{\rm{ \;}} = {\rm{ \;}}\left| {\vec a} \right|.\left| {\vec b} \right|\). A. \(\alpha {\rm{ \;}} = {180^0}.\) B. \(\alpha {\rm{ \;}} = {120^0}.\) C. \(\alpha {\rm{ \;}} = {90^0}.\) D. \(\alpha {\rm{ \;}} = {60^0}.\) Phần 2: Tự luận (4 điểm) Câu 1: Cho tam giác ABC. a) Tìm điểm K sao cho \(\overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {CB} \). b) Tìm điểm M sao cho \(\overrightarrow {MA} {\rm{ \;}} + 2\overrightarrow {MB} {\rm{ \;}} + 2\overrightarrow {MC} {\rm{ \;}} = \vec 0\). Câu 2: Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:
(Nguồn: https://nchmf.gov.vn) a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên. b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó. Câu 3: Chứng minh rằng với mọi tam giác ABC ta có a) \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\) b) \(\sin \frac{A}{2} = \sqrt {\frac{{(p - b)(p - c)}}{{bc}}} \)
----- HẾT ----- Lời giải HƯỚNG DẪN GIẢI CHI TIẾT THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1 (NB): Phương pháp: Mệnh đề là những khẳng định có tính đúng hoặc sai. Cách giải: Câu a) là câu cảm thán không phải là mệnh đề. Các câu b, c, d là mệnh đề => Có 3 mệnh đề. Chọn C. Câu 2 (NB): Phương pháp: Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà d nhỏ hơn 1 đơn vị của hàng đó. Cách giải: Vì độ chính xác đến hàng trăm (d = 123) nên ta làm tròn a đến hàng nghìn. Vậy số quy tròn của a là 23748000. Chọn B. Câu 3 (TH): Phương pháp: Biến đổi \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau. Xác định vị trí điểm M dựa vào điều kiện vừa tìm được. Cách giải:
Ta có \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \) \( \Rightarrow \) MABC là hình bình hành. Vì MABC là hình bình hành nên đáp án B, C đúng. Giả sử \(\overrightarrow {MA} = \overrightarrow {BC} \Rightarrow \overrightarrow {BC} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BC} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BC} + \overrightarrow {BC} = \overrightarrow 0 \Leftrightarrow 2\overrightarrow {BC} = \overrightarrow 0 \) \( \Rightarrow \) Sai. Chọn D. Câu 4 (NB): Phương pháp: Sử dụng định lí cosin trong tam giác tại đỉnh C: \({c^2} = {a^2} + {b^2} - 2ab\cos C\). Cách giải: Ta có: \({c^2} = {a^2} + {b^2} - 2ab\cos C\). \(\begin{array}{*{20}{l}}{ \Rightarrow A{B^2} = B{C^2} + A{C^2} - 2BC.AC.\cos C}\\{ \Rightarrow 5 = B{C^2} + 2 - 2.BC.\sqrt 2 .\frac{{\sqrt 2 }}{2}}\\{ \Leftrightarrow B{C^2} - 2BC - 3 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{BC = 3{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\\{BC = {\rm{ \;}} - 1{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.}\end{array}\) Vậy BC = 3. Chọn A. Câu 5 (NB): Phương pháp: Cặp số nào thỏa mãn bất phương trình là nghiệm của bất phương trình. Cách giải: Thay cặp số (x;y) = (0;4) vào bất phương trình: 0 – 2.4 + 5 > 0 => Sai. Thay cặp số (x;y) = (2;5) vào bất phương trình: 2 – 2. 5 + 5 > 0 => Sai. Thay cặp số (x;y) = (2;3) vào bất phương trình: 2 – 2.3 + 5 > 0 => Đúng. Thay cặp số (x;y) = (1;4) vào bất phương trình: 1 – 2.4 + 5 > 0 => Sai. Chọn C. Câu 6 (TH): Phương pháp: Biến đổi \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau. Xác định vị trí điểm M dựa vào điều kiện vừa tìm được. Cách giải:
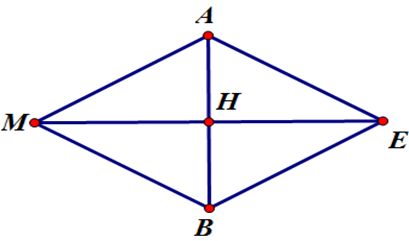
Ta có \(\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \) \( \Rightarrow \) MABC là hình bình hành. Giả sử \(\overrightarrow {MA} = \overrightarrow {BC} \Rightarrow \overrightarrow {BC} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BC} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BC} + \overrightarrow {BC} = \overrightarrow 0 \Leftrightarrow 2\overrightarrow {BC} = \overrightarrow 0 \) \( \Rightarrow \) Sai. Chọn D. Câu 7 (NB): Phương pháp: Tính \(\angle C = {180^0} - \left( {\angle A + \angle B} \right)\). Sử dụng định lí sin: \(\frac{c}{{\sin C}} = 2R\). Cách giải: Ta có: \(\angle C = {180^0} - \left( {\angle A + \angle B} \right) = {60^0}\). Áp dụng định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{6}{{2\sin {{60}^0}}} = 2\sqrt 3 \). Chọn B. Câu 8 (VD): Phương pháp: Sử dụng hệ quả định lí cosin. Cách giải: Ta có: \(\begin{array}{*{20}{l}}{\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}}\\{ = \frac{{{b^2} + {c^2} - {a^2}}}{{2bca}} + \frac{{{a^2} + {c^2} - {b^2}}}{{2acb}} + \frac{{{a^2} + {b^2} - {c^2}}}{{2abc}}}\\{ = \frac{{{b^2} + {c^2} - {a^2} + {a^2} + {c^2} - {b^2} + {a^2} + {b^2} - {c^2}}}{{2abc}}}\\{ = \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}}\end{array}\) Chọn A. Câu 9 (TH): Phương pháp: Giải phương trình, bất phương trình. Xác định tập hợp \(A\), \(B\) bằng phương pháp liệt kê phần tử, đưa về cách viết khoảng, nửa khoảng. Xác định \(A \cap B\); \(A \cup B\); \(A\backslash B\); \(B\backslash A\). Cách giải: *) \({x^2} - 7x + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 1 = 0}\\{x - 6 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 6}\end{array}} \right.\) (thỏa mãn) \( \Rightarrow A = \left\{ {1;{\mkern 1mu} {\mkern 1mu} 6} \right\}\) *) \(\left| x \right| > 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x < {\rm{\;}} - 4}\\{x > 4}\end{array}} \right.\)\( \Rightarrow x \in \left( { - \infty ;{\mkern 1mu} - 4} \right) \cup \left( {4;{\mkern 1mu} + \infty } \right)\) \( \Rightarrow B = \left( { - \infty ;{\mkern 1mu} - 4} \right) \cup \left( {4;{\mkern 1mu} + \infty } \right)\) Ta có: \(A \cup B = \left( { - \infty ;{\mkern 1mu} - 4} \right) \cup \left\{ 1 \right\} \cup \left( {4;{\mkern 1mu} + \infty } \right)\) , \(A \cap B = \left\{ 6 \right\}\) \(B\backslash A = \left( { - \infty ;{\mkern 1mu} - 4} \right) \cup \left( {4;{\mkern 1mu} {\mkern 1mu} 6} \right) \cup \left( {6; + \infty } \right)\), \(A\backslash B = \left\{ 1 \right\}\) Vậy đáp án đúng là: \(\left( {A\backslash B} \right) \subset A\) Chọn C. Câu 10 (TH): Phương pháp: Sử dụng khái niệm các phép toán trên tập hợp. Cách giải: Dễ thấy phần tô màu không thuộc A nên loại đáp án A, B. Phần tô màu trong hình vẽ biểu diễn cho tập hợp \(\left( {B \cap C} \right)\backslash A.\) Chọn D. Câu 11 (TH): Phương pháp: Tính PR và QR theo h = AR và \(\tan \alpha {\rm{ \;}} = \tan {65^0},{\mkern 1mu} {\mkern 1mu} \tan \beta {\rm{ \;}} = \tan {79^0}\). Sử dụng d = PQ = PR – QR, tính d. Tính chiều cao tòa nhà bằng d + RO. Cách giải: Đặt d = PQ = LM = 50m, h = AR là chiều cao từ giác kế đến đỉnh tòa nhà. Ta có: \(\angle APR = \alpha {\rm{ \;}} = {65^0},{\mkern 1mu} {\mkern 1mu} \angle AQR = \beta {\rm{ \;}} = {79^0}\). Gọi \({d_1} = PR = \frac{h}{{\tan \alpha }},{\mkern 1mu} {\mkern 1mu} {d_2} = QR = \frac{h}{{\tan \beta }}\), ta có: \(\begin{array}{*{20}{l}}{d = {d_1} - {d_2} = \frac{h}{{\tan \alpha }} - \frac{h}{{\tan \beta }} = h\left( {\frac{1}{{\tan \alpha }} - \frac{1}{{\tan \beta }}} \right)}\\{ \Rightarrow h = \frac{d}{{\frac{1}{{\tan \alpha }} - \frac{1}{{\tan \beta }}}} = \frac{{50}}{{\frac{1}{{\tan {{65}^0}}} - \frac{1}{{\tan {{79}^0}}}}} \approx 183,9{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}\) Vậy chiều cao của tòa nhà là AR + RO \( \approx 183,9 + 1,4 = 185,3{\mkern 1mu} {\mkern 1mu} \left( m \right)\). Chọn D. Câu 12 (TH): Phương pháp: Dùng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính cos x Cách giải: \(\begin{array}{*{20}{l}}{\sin x = \frac{1}{{\sqrt 3 }} \Rightarrow \sin {x^2} = \frac{1}{3} \Rightarrow {{\cos }^2}x = 1 - {{\sin }^2}x = 1 - \frac{1}{3} = \frac{2}{3}}\\{ \Rightarrow 2{{\sin }^2}x - {{\cos }^2}x = 2.\frac{1}{3} - \frac{2}{3} = 0}\end{array}\) Chọn B. Câu 13 (TH): Phương pháp: +) Giải phương trình, bất phương trình. +) Tìm giao của hai tập hợp tức là xác định các phần tử chung của hai tập hợp đó. Cách giải: *) Xét tập hợp \(A = \left\{ {x \in \mathbb{R}|\left( {2{x^2} - 7x + 5} \right)\left( {x - 2} \right) = 0} \right\}\). Ta có: \(\left( {2{x^2} - 7x + 5} \right)\left( {x - 2} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2{x^2} - 7x + 5 = 0}\\{x - 2 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{5}{2}}\\{x = 1}\\{x = 2}\end{array}} \right.\) (thỏa mãn) \( \Rightarrow A = \left\{ {1;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} \frac{5}{2}} \right\}\). *) Xét tâp hợp \(B = \left\{ {x \in \mathbb{Z}| - 3 < 2x + 1 < 5} \right\}\). Ta có: \( - 3 < 2x + 1 < 5 \Leftrightarrow {\rm{\;}} - 4 < 2x < 4 \Leftrightarrow {\rm{\;}} - 2 < x < 2\) Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ { - 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\). \( \Rightarrow B = \left\{ { - 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\). Vậy \(A \cap B = \left\{ 1 \right\}\). Chọn B. Câu 14 (TH): Phương pháp: Tìm \({\sin ^2}\alpha \) dựa vào đẳng thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Chia cả tử và mẫu của P cho \(\sin \alpha \), tính P theo \(\cos \alpha \) và \({\sin ^2}\alpha \). Cách giải: Chia cả tử và mẫu cho \(\sin \alpha {\rm{ \;}} \ne 0\) ta được: \(\begin{array}{*{20}{l}}{P = \frac{{\tan \alpha {\rm{ \;}} + 2\cot \alpha }}{{2\tan \alpha {\rm{ \;}} + 3\cot \alpha }}}\\{P = \frac{{\frac{1}{{\cos \alpha }} + \frac{{2\cos \alpha }}{{{{\sin }^2}\alpha }}}}{{\frac{2}{{\cos \alpha }} + \frac{{3\cos \alpha }}{{{{\sin }^2}\alpha }}}}}\end{array}\) Ta có: \(\begin{array}{*{20}{l}}{{{\sin }^2}\alpha {\rm{ \;}} + {{\cos }^2}\alpha {\rm{ \;}} = 1}\\{ \Rightarrow {{\sin }^2}\alpha {\rm{ \;}} + {{\left( {\frac{1}{4}} \right)}^2} = 1}\\{ \Leftrightarrow {{\sin }^2}\alpha {\rm{ \;}} = \frac{{15}}{{16}}}\end{array}\) Khi đó: \(P = \frac{{\frac{1}{{\frac{1}{4}}} + \frac{{2.\frac{1}{4}}}{{\frac{{15}}{{16}}}}}}{{\frac{2}{{\frac{1}{4}}} + \frac{{3.\frac{1}{4}}}{{\frac{{15}}{{16}}}}}} = \frac{{\frac{{68}}{{15}}}}{{\frac{{44}}{5}}} = \frac{{17}}{{33}}\). Chọn B. Câu 15 (TH): Phương pháp: Vì vật đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0\). Xác định \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} } \right|\), dựa vào tam giác MAB đều. Cách giải:
Ta có tam giác MAB đều. Do vật đứng yên nên ta có: \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0\)\( \Rightarrow \overrightarrow {{F_3}} {\rm{ \;}} = {\rm{ \;}} - (\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} )\)\( \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} } \right|\) \( \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {ME} } \right| = 2MH = 2.50\frac{{\sqrt 3 }}{2} = 50\sqrt 3 \) (với MAEB là hình bình hành tâm \(H\)). Chọn C. Câu 16 (TH): Phương pháp: Đặt \(\overrightarrow {AB} {\rm{ \;}} = \vec u\), \(\overrightarrow {BC} {\rm{ \;}} = \vec v\) suy ra \(\vec u + \vec v = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \). Xét các trường hợp A, B, C thẳng hàng; A, B, C không thẳng hàng. Ngoài ra, có thể chỉ ra các đáp án sai bằng cách chỉ ra một trường hợp mà mệnh đề đó không đúng. Cách giải: Đặt \(\overrightarrow {AB} {\rm{ \;}} = \vec u\), \(\overrightarrow {BC} {\rm{ \;}} = \vec v\) khi đó ta có \(\vec u + \vec v = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \) Nếu A,B,C thẳng hàng và \(B\) nằm giữa A,C thì \(\left| {\vec u + \vec v} \right| = \left| {\vec u} \right| + \left| {\vec v} \right|\) Nếu A,B,C thẳng hàng và \(B\)không nằm giữa A,C thì \(\left| {\vec u + \vec v} \right| < \left| {\vec u} \right| + \left| {\vec v} \right|\) Nếu A,B,C không thẳng hàng thì trong tam giác ABC có \(AB + BC > AC\). Suy ra \(\left| {\vec u + \vec v} \right| < \left| {\vec u} \right| + \left| {\vec v} \right|\) Do đó \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| + \left| {\vec v} \right|\) Từ đó suy ra, đáp án B đúng Đáp án A, C sai vì chọn \(\vec v = \vec 0\) thì có \(\left| {\vec u + \vec w} \right| \ge \left| {\vec u} \right| + \left| {\vec w} \right|\) (sai theo chứng minh ở trên). Đáp án D sai vì chọn \(\vec u = \vec 0\) và \(\vec v \ne \vec 0\) thì có \(\left| {\vec v} \right| \le {\rm{ \;}} - \left| {\vec v} \right|\)\( \Rightarrow \) vô lý vì độ dài véctơ khác vectơ-không là một số dương. Chọn B. Câu 17 (VD): Phương pháp: Tính số trung bình cộng để so sánh tuổi thọ của từng loại bút. Tính phương sai, độ lệch chuẩn để so sánh sự đồng đều về chất lượng của từng loại bút. Cách giải: *) Loại bút A: Số trung bình: \(\overline {{x_{\rm{A}}}} {\rm{\;}} = \frac{{23 + 25 + 27 + 28 + 30 + 35}}{6} = 28\) (giờ) Phương sai: \(s_A^2 = \frac{1}{6}\left[ {{{\left( {23 - 28} \right)}^2} + {{\left( {25 - 28} \right)}^2} + {{\left( {27 - 28} \right)}^2} + {{\left( {28 - 28} \right)}^2} + {{\left( {30 - 28} \right)}^2} + {{\left( {35 - 28} \right)}^2}} \right] \approx 14,7\) (giờ) Độ lệch chuẩn: \({s_A} = \sqrt {s_A^2} {\rm{\;}} = \sqrt {14,7} {\rm{\;}} \approx 3,83\) (giờ) *) Loại bút B: Số trung bình: \(\overline {{x_B}} {\rm{\;}} = \frac{{16 + 22 + 28 + 33 + 46}}{5} = 29\) (giờ) Phương sai: \(s_B^2 = \frac{1}{5}\left[ {{{\left( {16 - 29} \right)}^2} + {{\left( {22 - 29} \right)}^2} + {{\left( {28 - 29} \right)}^2} + {{\left( {33 - 29} \right)}^2} + {{\left( {46 - 29} \right)}^2}} \right] = 104,8\) (giờ) Độ lệch chuẩn: \({s_B} = \sqrt {s_B^2} {\rm{\;}} = \sqrt {104,8} {\rm{\;}} \approx 10,24\) (giờ) Vì \(\overline {{x_{\rm{A}}}} {\rm{\;}} < \overline {{x_B}} \) nên loại bút B có thời gian sử dụng lâu hơn. Vì \(s_A^2 < s_B^2\) và \(s_A^{} < s_B^{}\) nên chất lượng của bút B không đồng đều. Vậy loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B không đồng đều. Chọn C. Câu 18 (NB): Phương pháp: Áp dụng lý thuyết về phương sai và độ lệch chuẩn. Cách giải: Ta có: \(s = \sqrt {{s^2}} \) với \(s\) là độ lệch chuẩn và \({s^2}\) là phương sai của số liệu thống kê. Chọn D. Câu 19 (TH): Phương pháp: Sử dụng công thức: \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right).\) Cách giải: Vì ABC là tam giác vuông cân tại A nên \(BC = AB\sqrt 2 {\rm{ \;}} = 6\sqrt 2 \) và \(\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \angle ABC = {45^0}\). Vậy \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\) \( = 6.6\sqrt 2 .\cos {45^0} = 6.6\sqrt 2 .\frac{{\sqrt 2 }}{2} = 36.\) Chọn B. Câu 20 (TH): Phương pháp: - Mốt là giá trị có tần số lớn nhất trong bảng số liệu, kí hiệu là \({M_0}\) - Xác định số trung vị: Sắp xếp mẫu số liệu kích thước \(N\) theo thứ tự không giảm (tăng dần) hoặc không tăng (giảm dần): + Nếu \(N\) lẻ \( \Rightarrow {M_e} = \) số đứng thứ \(\frac{{N + 1}}{2}\) (chính giữa) + Nếu \(N\) chẵn \( \Rightarrow {M_e} = \) trung bình cộng hai số đứng giữa là \(\frac{N}{2}\) và \(\frac{N}{2} + 1\) Cách giải: Bảng phân bố tần số, sắp xếp theo thứ tự tăn dần về thời gian: +) Vì \(x = 1\) có tần số lớn nhất \(n = 2\)\( \Rightarrow {M_0} = 1\) là Mốt của bảng số liệu trên. +) Vì \(N = 9\) (lẻ) \( \Rightarrow \) Số trung vị \({M_e} = {x_{\frac{{N + 1}}{2}}} = {x_5} = 1,5\) (phút) Chọn C. Câu 21 (NB): Phương pháp: Xét điểm gốc tọa độ để xác định miền nghiệm của bất phương trình. Cách giải: Thay \(x = 0,y = 0\) vào BPT \(2x - 3y + 6 \ge 0\) ta được: \(2.0 - 3.0 + 6 \ge 0\) (đúng) Nên O(0,0) thuộc miền nghiệm nên Miền nghiệm nửa mặt phẳng có bờ là d chứa gốc tọa độ O và có lấy đường thẳng d Chọn A. Câu 22 (NB): Phương pháp: Vẽ đồ thị hoặc thử các đáp án Cách giải: Xét hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > - 3\quad (1)}\\{3x - y < 5\quad (2)}\\{y - 1 > 0\quad (3)}\end{array}} \right.\). \(\left( { - 2; - 1} \right)\) không thỏa mãn BPT (3) \(\left( {2;0} \right)\) không thỏa mãn BPT (3) \(\left( {3;2} \right)\) không thỏa mãn BPT (2) \(\left( {0,2} \right)\)thỏa mãn cả 3 BPT nên là nghiệm của hệ. Chọn D. Câu 23 (TH): Phương pháp: Nhóm thích hợp, sử dụng mối quan hệ giá trị lượng giác của hai góc bù nhau: \(\cos \left( {{{180}^0} - \alpha } \right) = {\rm{ \;}} - \cos \alpha \). Cách giải: \(\begin{array}{*{20}{l}}{B = \cos {0^0} + \cos {{20}^0} + \cos {{40}^0} + ... + \cos {{160}^0} + \cos {{180}^0}}\\{B = \left( {\cos {0^0} + \cos {{180}^0}} \right) + \left( {\cos {{20}^0} + \cos {{160}^0}} \right) + \left( {\cos {{40}^0} + \cos {{140}^0}} \right) + ... + \left( {\cos {{80}^0} + \cos {{100}^0}} \right)}\\{B = \left( {\cos {0^0} - \cos {0^0}} \right) + \left( {\cos {{20}^0} - \cos {{20}^0}} \right) + \left( {\cos {{40}^0} - \cos {{40}^0}} \right) + ... + \left( {\cos {{80}^0} - \cos {{80}^0}} \right)}\\{B = 0}\end{array}\) Chọn A Câu 24 (TH): Phương pháp: Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\) Cách giải: Ta có: \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} - \frac{1}{3}\overrightarrow {BC} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} - \frac{1}{3}BC.BA.\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right).\) Vì tam giác ABC đều nên \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \angle ABC = {60^0}\). \( \Rightarrow \overrightarrow {BM} .\overrightarrow {BA} = - \frac{1}{3}.6.6.\frac{{1 }}{2} = {\rm{ \;}} - 6.\) Chọn D. Câu 25 (NB): Phương pháp: Xác định số gần đúng a và độ chính xác d. Tính số đúng \(\bar a = a \pm d \Rightarrow a - d \le \bar a \le a + d\). Cách giải: Gọi \(\bar a\) là độ dài đúng của dây cầu \( \Rightarrow \bar a = 996m \pm 0,5m\). \(\begin{array}{*{20}{l}}{ \Rightarrow 996 - 0,5 \le \bar a \le 996 + 0,5}\\{ \Leftrightarrow 995,5 \le \bar a \le 996,5}\end{array}\) Vậy độ dài đúng của cầu là một số nằm trong khoảng 995,5m đến 996,5m. Chọn A. Câu 26 (TH): Phương pháp: Tính diện tích hình chữ nhật bằng dài nhân rộng. Sai số tương đối \({\delta _a} \le \frac{d}{{\left| a \right|}}\). Cách giải: Diện tích hình chữ nhật là: \(\begin{array}{l}S = \left( {2m \pm 0,01m} \right)\left( {5m \pm 0,02m} \right)\\\,\,\,\, = \left( {2.5{m^2} \pm \left( {2.0,02 + 5.0,01 + 0,01.0,02} \right){m^2}} \right)\\\,\,\,\, = \left( {10{m^2} \pm 0,0902{m^2}} \right)\end{array}\) \( \Rightarrow a = 10,\,\,d = 0,0902\). \( \Rightarrow {\delta _a} \le \frac{d}{{\left| a \right|}} = \frac{{0,0902}}{{10}} = 0,00902 = 0,902\) ‰. Chọn C. Câu 27 (TH): Phương pháp: Khoảng biến thiên, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu. Cách giải: Giá trị lớn nhất trong mẫu số liệu là 20. Giá trị nhỏ nhất trong mẫu số liệu là 5. Vậy khoảng biến thiên R = 20 – 5 = 15. Chọn C. Câu 28 (VD): Phương pháp: Sử dụng công thức \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\). Cách giải: Gọi A là tập hợp các bạn đăng kí tiết mục múa \( \Rightarrow n\left( A \right) = 9.\) B là tập hợp các bạn đăng kí tiết mục diễn kịch \( \Rightarrow n\left( B \right) = 13.\) \( \Rightarrow A \cap B:\) tập hợp các bạn đăng kí cả 2 tiết mục múa và diễn kịch \( \Rightarrow n\left( {A \cap B} \right) = 4.\) \(A \cup B\): tập hợp các bạn tham gia ít nhất 1 tiết mục. Ta có: \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\) \( \Rightarrow \) Số học sinh lớp 10A tham gia văn nghệ là: \(n\left( {A \cup B} \right) = 9 + 13 - 4 = 18.\) Chọn B. Câu 29 (TH): Phương pháp: Gọi M là trung điểm BC. Sử dụng tính chất trung điểm. Cách giải:
Gọi \(M\) là trung điểm BC. Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = 2\sqrt {A{B^2} + B{M^2}} {\rm{ \;}} = 2\sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} {\rm{ \;}} = a\sqrt 5 \). Chọn D. Câu 30 (TH): Phương pháp: Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\). Cách giải: Ta có: \(\begin{array}{l}\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow 2\vec a.\vec b = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right| = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right|\left[ {2\cos \left( {\vec a,\vec b} \right) - 1} \right] = 0\\ \Leftrightarrow \cos \left( {\vec a,\vec b} \right) = \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \vec a \ne \vec 0,{\mkern 1mu} {\mkern 1mu} \vec b \ne \vec 0} \right)\end{array}\) \( \Leftrightarrow \left( {\vec a,\vec b} \right) = {60^0}.\) Chọn D.
Phần 2: Tự luận (4 điểm) Câu 1 (VD): Phương pháp: a) Sử dụng quy tắc hiệu, đưa về tính chất vectơ trọng tâm tam giác. b) Sử dụng tính chất vectơ trung tuyến. Cách giải: a) Ta có: \(\begin{array}{*{20}{l}}{\overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {CB} }\\{ \Leftrightarrow \overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {KB} {\rm{ \;}} - \overrightarrow {KC} }\\{ \Leftrightarrow \overrightarrow {KA} {\rm{ \;}} + \overrightarrow {KB} {\rm{ \;}} + \overrightarrow {KC} {\rm{ \;}} = \vec 0}\end{array}\) Vậy K là trọng tâm tam giác ABC. b) Gọi I là trung điểm của BC ta có: \(\begin{array}{l}\overrightarrow {MA} + 2\overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA} + 2\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = \overrightarrow 0 \\ \Leftrightarrow \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) + 4\overrightarrow {MI} = \overrightarrow 0 \\ \Leftrightarrow 5\overrightarrow {MI} + \overrightarrow {IA} = 0\\ \Leftrightarrow \overrightarrow {IM} = \frac{1}{5}\overrightarrow {IA} \end{array}\) Vậy M là thuộc IA sao cho \(IM = \frac{1}{5}IA\). Câu 2 (VD): Phương pháp: Tính giá trị trung bình \(\bar x\). Phương sai \({s^2} = \frac{{{{\left( {{x_1} - \bar x} \right)}^2} + {{\left( {{x_2} - \bar x} \right)}^2} + ... + {{\left( {{x_n} - \bar x} \right)}^2}}}{n}\). Độ lệch chuẩn \(s = \sqrt {{s^2}} \). Cách giải: a) Mẫu số liệu: 23 25 26 27 27 27 27 21 19 18 b) Số trung bình cộng: \(\bar x = \frac{{23 + 25 + 26 + 27 + 27 + 27 + 27 + 21 + 19 + 18}}{{10}} = 24\) (0C). Phương sai: \({s^2} = \frac{{{{\left( {23 - 24} \right)}^2} + {{\left( {25 - 24} \right)}^2} + 4.{{\left( {27 - 24} \right)}^2} + {{\left( {26 - 24} \right)}^2} + {{\left( {21 - 24} \right)}^2} + {{\left( {19 - 24} \right)}^2} + {{\left( {18 - 24} \right)}^2}}}{{10}} = 11,2\) Độ lệch chuẩn: \(s = \sqrt {{s^2}} {\rm{ \;}} = \sqrt {11,2} {\rm{ \;}} = \frac{{2\sqrt {70} }}{5} \approx 3,35\). Câu 3 (VDC): Phương pháp: a) Áp dụng định lí cosin và định lí sin b) Áp dụn định lí cosin và công thức \(\cos A = 1 - 2{\sin ^2}\frac{A}{2}\) Cách giải: a) Áp dụng định lí cosin và định lí sin ta có: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\sin A = \frac{a}{{2R}}\) \( \Rightarrow \cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}.\frac{{2R}}{a} = \frac{{{b^2} + {c^2} - {a^2}}}{{abc}}R\) Tương tự ta cũng có: \(\cot B = \frac{{{a^2} + {c^2} - {b^2}}}{{abc}}R;\cot C = \frac{{{a^2} + {b^2} - {c^2}}}{{abc}}R\)
\(\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{{{b^2} + {c^2} - {a^2}}}{{abc}}R + \frac{{{a^2} + {c^2} - {b^2}}}{{abc}}R + \frac{{{a^2} + {b^2} - {c^2}}}{{abc}}R\\ = \frac{R}{{abc}}({b^2} + {c^2} - {a^2} + {a^2} + {c^2} - {b^2} + {a^2} + {b^2} - {c^2})\\ = \frac{R}{{abc}}({a^2} + {b^2} + {c^2}) = \frac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\end{array}\) b) Ta có: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\) Mà \(\cos A = 1 - 2{\sin ^2}\frac{A}{2} \Rightarrow \sin \frac{A}{2} = \sqrt {\frac{{1 - \cos A}}{2}} \) (do \({0^ \circ } < \frac{A}{2} < {90^ \circ }\)) \(\begin{array}{l} \Rightarrow \sin \frac{A}{2} = \sqrt {\frac{{1 - \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}}{2}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{{a^2} - \left( {{b^2} + {c^2} - 2bc} \right)}}{{4bc}}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{{a^2} - {{(b - c)}^2}}}{{4bc}}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{(a - b + c)(a + b - c)}}{{4bc}}} \end{array}\) Lại có: \(p = \frac{{a + b + c}}{2}\)\( \Rightarrow p - b = \frac{{a - b + c}}{2};p - c = \frac{{a + b - c}}{2}\) \(\begin{array}{l} \Leftrightarrow \frac{{(a - b + c)(a + b - c)}}{4} = (p - b)(p - c)\\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{(p - b)(p - c)}}{{bc}}} \end{array}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
