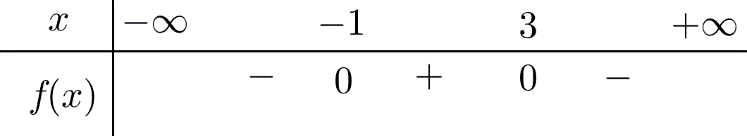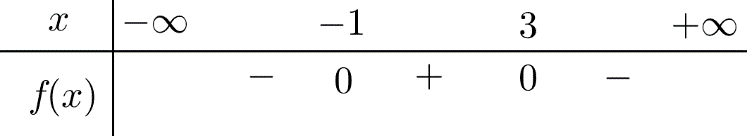Đề kiểm tra học kì 2 Toán 10 - Đề số 2 - Kết nối tri thứcTải về I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm). Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
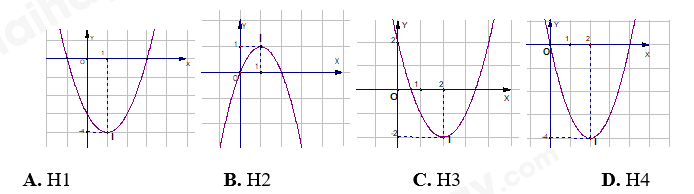
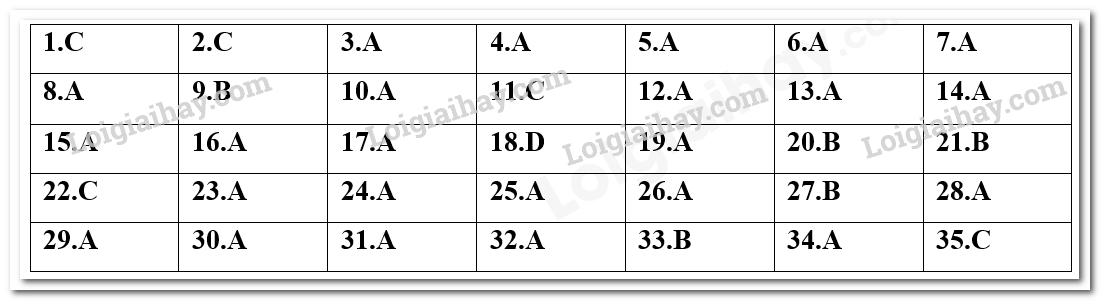
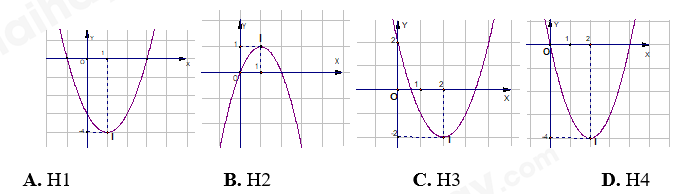
Đề bài I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm). Câu 1: Cho hàm số \(y = \left\{ \begin{array}{l}x + 1,\,\,khi\,\,x \ge 2\\2 - x,\,\,khi\,\,x < 1\end{array} \right.\),Tính giá trị của hàm số tại \(3\). A. 3. B. -1. C. 4. D. 1. Câu 2: Hàm số \(y = {x^2} - 4x + 2\) có đồ thị là hình vẽ nào sau đây?
Câu 3: Có bao nhiêu giá trị \(m\)nguyên để \(f(x) = {x^2} + (m + 1)x - m > 0,\,\forall x \in \mathbb{R}.\) A. 5. B. 4. C. 6. D. 3. Câu 4: Tổng các nghiệm của phương trình \(\sqrt {{x^2} + 2x + 1} = 2x - 1\) bằng A. 2. B. 3. C. 4. D. 1. Câu 5: Viết phương trình đường thẳng \(d\) song song với \(d':x + 2y - 1 = 0\) và cách \(d'\) một khoảng bằng \(\sqrt 5 \). A. \(x + 2y + 4 = 0\) hoặc \(x + 2y - 6 = 0\). B. \(x + 2y + 4 = 0\). C. \(x + 2y - 6 = 0\). D. \(x + 2y + \sqrt 5 = 0\). Câu 6: Viết phương trình đường thẳng \(d \bot d':x - y + 1 = 0\)và đi qua điểm \(A(1;\,\,2).\) A. \(x + y - 3 = 0\). B. \(x + y + 3 = 0\). C. \( - x + y - 1 = 0\). D. \( - x - y - 3 = 0\). Câu 7: Viết phương trình đường tròn đường kính \(AB\), với \(A(1;\,3);\,\,B( - 2; - 1)\). A. \({\left( {x + \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{25}}{4}\). B. \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + 1} \right)^2} = \frac{{25}}{4}\) C. \({\left( {x + \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} = 25\). D. \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + 1} \right)^2} = 25\). Câu 8: Cho tam giác \(ABC\)có \(A(2;0);\,\,B( - 1;0);\,\,C(1;2)\), viết phương trình đường tròn ngoại tiếp tam giác \(ABC\). A. \({x^2} + {y^2} - x - y - 2 = 0\). B. \({x^2} + {y^2} - x - y + 2 = 0\). C. \({x^2} + {y^2} + x + y + 2 = 0\). D. \({x^2} + {y^2} + x - y - 2 = 0\). Câu 9: Cho hai điểm \({F_1}\) và \({F_2}\) cố định và một độ dài không đổi \(2a\) lớn hơn \({F_1}{F_2}.\) Mệnh đề nào dưới đây đúng? A. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} - M{F_2} = 2a.\) B. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a.\) C. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} = M{F_2}.\) D. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} + M{F_2} = a.\) Câu 10: Có 10 hộp sữa trong đó có 3 hộp bị hỏng. Chọn ngẫu nhiên 4 hộp, xác suất để lấy được 4 hộp mà không có hộp nào bị hỏng? A. \(\frac{1}{6}\) B. \(\frac{{41}}{{42}}\) C. \(\frac{1}{{21}}\) D. \(\frac{1}{{41}}\) Câu 11: Một túi có 15 viên bi trong đó có 7 bi đỏ, 5 bi xanh và 3 bi vàng. Số cách chọn hai viên bi khác màu là A. 105. B. 210. C. 71. D. 74. Câu 12: Có bao nhiêu số tự nhiên có 2 chữ số khác nhau được lập từ tập \(A = {\rm{\{ 0;1;2;5;7\} }}\) A. 16 B. 20 C. 25 D. 26 Câu 13: Gieo 3 đồng xu cân đối đồng chất mô tả không gian mẫu của phép thử: A. {NNN, SSS, NNS, SSN, NSN, SNS, NSS, SNN}. B. {NNN, SSS, NNS, SSN, NSN, SNS}. C. {NN, NS, SN, SS}. D. {NNN, SSS, NNS, SSN, NSN, NSS, SNN}. Câu 14: Rút ra hai lá bài từ cỗ bài tú lơ khơ 52 lá. Xác suất để rút được ít nhất một lá ách (A) là bao nhiêu? A. \(\frac{{33}}{{221}}\). B. \(\frac{{32}}{{221}}\). C. \(\frac{1}{{221}}\). D. \(\frac{1}{{1326}}\). Câu 15: Gieo một con súc sắc cân đối đồng chất hai lần. Xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 10 bằng bao nhiêu? A. \(\frac{5}{6}\). B. \(\frac{1}{6}\). C. \(\frac{1}{{36}}\). D. \(\frac{7}{{36}}\). Câu 16: Hàm số \(y = f(x)\)được gọi là đồng biến trên \((a;b)\)nếu: A. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\). B. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\). C. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) \le f({x_2})\). D. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) \ge f({x_2})\). Câu 17: Hoành độ đỉnh của Parabol \(y = a{x^2} + bx + c\)\((a \ne 0)\)có công thức: A. \(\frac{{ - b}}{{2a}}\). B. \(\frac{b}{{2a}}\). C. \(\frac{{ - b}}{a}\). D. \(\frac{b}{a}\). Câu 18: Bạn An giải phương trình \(\sqrt { - {x^2} + 2x + 4} = x - 2\) như sau: Bước 1: Bình phương 2 vế ta có PT hệ quả: \( - {x^2} + 2x + 4 = {(x - 2)^2}\) Bước 2: Thu gọn ta được PT: \( - 2{x^2} + 6x = 0\). Giải và tìm được \(x = 0\)hoặc \(x = 3\). Bước 3: Kết luận tập nghiệm của PT là \(S = \left\{ {0;3} \right\}\) Bài làm của bạn An đúng hay sai? A. Đúng. B. Sai từ Bước 1. C. Sai từ Bước 2. D. Sai từ Bước 3. Câu 19: Cho tam thức bậc hai \(f\left( x \right)\) có bảng xét dấu như sau
Mệnh đề nào dưới đây đúng? A. \(f\left( x \right) \ge 0\, \Leftrightarrow - 1 \le x \le 3.\) B. \(f\left( x \right) \ge 0\, \Leftrightarrow - 1 < x < 3.\) C. \(f\left( x \right) \ge 0\, \Leftrightarrow x > 3.\) D. \(f\left( x \right) \ge 0\, \Leftrightarrow x < - 1.\) Câu 20: Một véc tơ pháp tuyến của đường thẳng \(y = 3x - 2\) A. \(\overrightarrow n = (3;1)\). B. \(\overrightarrow n = (3; - 1)\). C. \(\overrightarrow n = (3; - 2)\). D. \(\overrightarrow n = (3;2)\). Câu 21: Phương trình tham số của đường thẳng \(\Delta \) đi qua \(M({x_0};{y_0})\)và có Véc tơ chỉ phương \(\overrightarrow u = (a;b)\): A. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\). B. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} - bt}\end{array}} \right.\). C. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + bt}\\{y = {y_0} + at}\end{array}} \right.\) D. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} - bt}\\{y = {y_0} - at}\end{array}} \right.\). Câu 22: Có bao nhiêu vị trí tương đối giữa hai đường thẳng trong mặt phẳng? A. 1. B. 2. C. 3. D. 4. Câu 23: Trong mặt phẳng tọa độ \(Oxy\),Elip \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\)có độ dài tiêu cự: A. \(2\sqrt {{a^2} - {b^2}} \). B. \(\sqrt {2{a^2} - {b^2}} \). C. \(\sqrt {{a^2} - {b^2}} \). D. \(\sqrt {2{a^2} - 2{b^2}} \). Câu 24: Xác định công thức đúng. A. \(A_n^k = \frac{{n!}}{{(n - k)!}}\). B. \(A_n^k = \frac{{n!}}{{(n - k)!k!}}\). C. \(A_n^k = \frac{{k!}}{{(n - k)!k!}}\). D. \(A_n^k = \frac{{k!}}{{(n - k)!n!}}\) Câu 25: Số tập hợp con của tập hợp có \(n\)phần tử A. \({2^n}\). B. \(2n\). C. \({3^n}\). D. \(3n\). Câu 26: Có bao nhiêu cách sắp xếp 3 bạn vào một ghế dài 3 chỗ ngồi. A. 6. B. 12. C. 9. D. 27. Câu 27: Minh có 3 cái áo sơ mi và 5 cái quần. Số cách để minh phối một bộ đồ (gồm 1 áo và 1 quần) là: A. 8. B. 15. C. 2. D. 45. Câu 28: Gieo 1 con súc sắc 2 lần thì có thể có bao nhiêu kết quả xảy ra? A. 36. B. 12. C. 6. D. 4. Câu 29: Hệ số trong khai triển \({(a + b)^4}\)là: A. 1;4;6;4;1. B. 1;3;3;1. C. 1;5;10;10;5;1. D. 1;2;4;2;1. Câu 30: Tìm tâm và bán kính của đường tròn có phương trình \({x^2} + {y^2} - 2x - 2y + 1 = 0\). A. \(I(1;1);\,\,R = 1.\) B. \(I( - 1; - 1);\,\,R = 1.\) C. \(I(1;1);\,\,R = 3.\) D. \(I( - 1; - 1);\,\,R = - 1.\) Câu 31: Trong các phương trình sau phương trình nào là phương trình đường tròn A. \({x^2} + {y^2} + 2x + 2y - 3 = 0\). B. \({x^2} + {y^2} + 2x + 2y + 3 = 0\). C. \(2{x^2} + {y^2} + 2x + 2y - 3 = 0\). D. \({x^2} - {y^2} + 2x + 2y - 3 = 0\). Câu 32: Một hộp chứa 5 viên bi xanh, 4 viên bi đỏ. Lấy ra hai viên bi. Tính xác suất để hai viên bi được lấy ra là hai bi đỏ. A. \(\frac{1}{6}\). B. \(\frac{4}{9}\). C. \(\frac{5}{9}\). D. \(\frac{5}{{18}}\). Câu 33: Có bao nhiêu cách xếp 10 người vào một bàn tròn A. 10!. B. 9! C. 8!. D. 11!. Câu 34: Trong thùng xăm có 25 xăm tốt, 15 xăm xấu; anh An rút một xăm. Tính xác suất để anh An rút được xăm tốt. A. \(\frac{5}{8}\). B. \(\frac{3}{8}\). C. \(\frac{8}{5}\). D. \(\frac{8}{3}\). Câu 35: Trong mặt phẳng \(Oxy,\) cho hai đường thẳng \({d_1}:\, - x + y + 1 = 0\) và \({d_2}:2\,x + 2y - 3 = 0.\) Góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) bằng A. \(45^\circ .\) B. \(60^\circ .\) C. \(90^\circ .\) D. \(30^\circ .\) II. TỰ LUẬN(4câu - 3,0 điểm). Câu 36: Giải phương trình sau \(\sqrt {2x + 2\sqrt {2x - 1} } = x + 1\) Câu 37: Trong mặt phẳng \(Oxy,\) cho điểm \(A\left( {1;\,2} \right),\,B( - 1;1)\)và đường thẳng \(d:x - y + 3 = 0\). Tìm tọa độ điểm \(M \in d\) để \(AM + BM\) nhỏ nhất. Câu 38: Trong mặt phẳng \(Oxy,\) cho tam giác \(ABC\) có \(A(2;1)\). Đường cao đi qua \(B\) có phương trình \(x - 3y - 7 = 0\), đường trung tuyến qua đỉnh \(C\)có phương trình \(x + y + 1 = 0\). Xác định tọa độ điểm \(B,\,C\). Câu 39: Tìm \(m\) để \(f(x) = ({m^2} - 1){x^2} + (m - 1)x - 2m - 1 < 0,\,\,\forall x \in \mathbb{R}\). ---------- HẾT ---------- Lời giải HƯỚNG DẪN GIẢI CHI TIẾT THỰC HIỆN: BAN CHYÊN MÔN LOIGIAIHAY.COM I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm). Câu 1: Cho hàm số \(y = \left\{ \begin{array}{l}x + 1,\,\,khi\,\,x \ge 2\\2 - x,\,\,khi\,\,x < 1\end{array} \right.\),Tính giá trị của hàm số tại \(3\). A. 3. B. -1. C. 4. D. 1. Phương pháp - Thay x vào hàm số đã cho. Lời giải Vì \(x = 3 > 2\) nên giá trị của hàm số tại 3 bằng 4 Chọn C Câu 2: Hàm số \(y = {x^2} - 4x + 2\) có đồ thị là hình vẽ nào sau đây? Phương pháp Hình dáng của đồ thị bậc hai Parabol. Lời giải Vì \(a = 1 > 0\) nên bề lõm quay lên trên Mặt khác hàm số có tọa độ đỉnh là \(I(2; - 2)\), khi \(x = 0 \Rightarrow y = 2\) Chọn C Câu 3: Có bao nhiêu giá trị \(m\)nguyên để \(f(x) = {x^2} + (m + 1)x - m > 0,\,\forall x \in \mathbb{R}.\) A. 5. B. 4. C. 6. D. 3. Phương pháp Sử dụng công thức dấu của tam thức bậc hai. Lời giải \(\begin{array}{l}f(x) = {x^2} + (m + 1)x - m > 0,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right. \Leftrightarrow {m^2} + 2m + 1 + 4m < 0\\ \Leftrightarrow - 3 - 2\sqrt 2 < m < - 3 + 2\sqrt 2 \end{array}\) Vậy có 5 giá trị nguyên thỏa yêu cầu bài toán. Chọn A Câu 4: Tổng các nghiệm của phương trình \(\sqrt {{x^2} + 2x + 1} = 2x - 1\) bằng A. 2. B. 3. C. 4. D. 1. Phương pháp Bình phương hai vế của phương trình rồi giải. Lời giải \(\sqrt {{x^2} + 2x + 1} = 2x - 1 \Leftrightarrow \left\{ \begin{array}{l}2x - 1 \ge 0\\{x^2} + 2x + 1 = 4{x^2} - 4x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{2}\\3{x^2} - 6x = 0\end{array} \right. \Leftrightarrow x = 2\). Tổng các nghiệm của phương trình là \(2\). Chọn A Câu 5: Viết phương trình đường thẳng \(d\) song song với \(d':x + 2y - 1 = 0\) và cách \(d'\) một khoảng bằng \(\sqrt 5 \). A. \(x + 2y + 4 = 0\) hoặc \(x + 2y - 6 = 0\). B. \(x + 2y + 4 = 0\). C. \(x + 2y - 6 = 0\). D. \(x + 2y + \sqrt 5 = 0\). Phương pháp Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) Lời giải \(d\) song song với \(d'\) nên \(d:x + 2y + m = 0\). \(A(1;0) \in d'\) \(d(d,d') = d(A,d) = \frac{{\left| {1 + 2.0 + m} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \sqrt 5 \Leftrightarrow \left[ \begin{array}{l}m + 1 = 5\\m + 1 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 4\\m = - 6\end{array} \right..\) Chọn A Câu 6: Viết phương trình đường thẳng \(d \bot d':x - y + 1 = 0\)và đi qua điểm \(A(1;\,\,2).\) A. \(x + y - 3 = 0\). B. \(x + y + 3 = 0\). C. \( - x + y - 1 = 0\). D. \( - x - y - 3 = 0\). Phương pháp Phương trình tổng quát của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vecto pháp tuyến là : \(d:a(x - {x_0}) + b(y - {y_0}) = 0\) Lời giải Vì \(d \bot d'\) nên \(d\) có dạng \(x + y + m = 0\) Mặt khác \(A \in d\) nên \(1 + 2 + m = 0 \Leftrightarrow m = - 3\). Chọn A Câu 7: Viết phương trình đường tròn đường kính \(AB\), với \(A(1;\,3);\,\,B( - 2; - 1)\). A. \({\left( {x + \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{25}}{4}\). B. \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + 1} \right)^2} = \frac{{25}}{4}\) C. \({\left( {x + \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} = 25\). D. \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + 1} \right)^2} = 25\). Phương pháp Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\) Lời giải Ta có \(\overrightarrow {AB} = ( - 3; - 4) \Rightarrow AB = 5\). Suy ra bán kính đường tròn đường kính \(AB\)là \(R = \frac{5}{2}\). Tọa độ trung điểm \(I\) của \(AB\) là \(I\left( {\frac{{ - 1}}{2};1} \right)\). Phương trình đường tròn cần tìm là \({\left( {x + \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{25}}{4}\). Chọn A Câu 8: Cho tam giác \(ABC\)có \(A(2;0);\,\,B( - 1;0);\,\,C(1;2)\), viết phương trình đường tròn ngoại tiếp tam giác \(ABC\). A. \({x^2} + {y^2} - x - y - 2 = 0\). B. \({x^2} + {y^2} - x - y + 2 = 0\). C. \({x^2} + {y^2} + x + y + 2 = 0\). D. \({x^2} + {y^2} + x - y - 2 = 0\). Phương pháp Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\) Lời giải Phương trình đường tròn cần tìm có dạng \({x^2} + {y^2} + a.x + b.y + c = 0\) Vì đường tròn ngoại tiếp tam giác \(ABC\) nên ta có \(\left\{ \begin{array}{l}2a + c = - 4\\ - a + c = - 1\\a + 2b + c = - 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = - 1\\c = - 2\end{array} \right.\) Vậy phương trình đường tròn cần tìm có dạng \({x^2} + {y^2} - x - y - 2 = 0\) Chọn A Câu 9: Cho hai điểm \({F_1}\) và \({F_2}\) cố định và một độ dài không đổi \(2a\) lớn hơn \({F_1}{F_2}.\) Mệnh đề nào dưới đây đúng? A. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} - M{F_2} = 2a.\) B. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a.\) C. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} = M{F_2}.\) D. Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} + M{F_2} = a.\) Phương pháp Định nghĩa của Elip Lời giải Chọn B Elip là tập hợp tất cả các điểm \(M\) trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a.\) Câu 10: Có 10 hộp sữa trong đó có 3 hộp bị hỏng. Chọn ngẫu nhiên 4 hộp, xác suất để lấy được 4 hộp mà không có hộp nào bị hỏng? A. \(\frac{1}{6}\) B. \(\frac{{41}}{{42}}\) C. \(\frac{1}{{21}}\) D. \(\frac{1}{{41}}\) Phương pháp Công thức tính xác suất Lời giải Số phần tử của không gian mẫu là \(n(\Omega ) = C_{10}^4 = 210\). Gọi A là biến cố chọn 4 hộp mà không có hộp nào hỏng Số phần tử của biến cố A là \(n(A) = C_7^4 = 35\). Xác suất để lấy được 4 hộp mà không có hộp nào hỏng là \(P = \frac{{n(A)}}{{n(\Omega )}} = \frac{{35}}{{210}} = \frac{1}{6}\) Chọn A Câu 11: Một túi có 15 viên bi trong đó có 7 bi đỏ, 5 bi xanh và 3 bi vàng. Số cách chọn hai viên bi khác màu là A. 105. B. 210. C. 71. D. 74. Phương pháp Áp dụng công thức tổ hợp Lời giải. Chọn hai viên bi khác màu ta sẽ có các trường hợp sau TH 1: 1 bi đỏ; 1 bi xanh Chọn một bi đỏ, một viên bi xanh có \(C_7^1.C_5^1 = 35\) cách chọn TH 2: 1 bi đỏ; 1 bi vàng Chọn một bi đỏ, một viên bi vàng có \(C_7^1.C_3^1 = 21\) cách chọn TH 3: 1 bi xanh; 1 bi vàng Chọn một bi đỏ, một viên bi vàng có \(C_5^1.C_3^1 = 15\) cách chọn Vậy để chọn 2 viên bi trong 15 viên bi khác màu là:\(35 + 21 + 15 = 71\). Chọn C Câu 12: Có bao nhiêu số tự nhiên có 2 chữ số khác nhau được lập từ tập \(A = {\rm{\{ 0;1;2;5;7\} }}\) A. 16 B. 20 C. 25 D. 26. Phương pháp Áp dụng quy tắc nhân Lời giải: Gọi số tự nhiên cần tìm có dạng \(\overline {ab} \) Chọn \(a\) có bốn cách chọn Chọn \(b\) có bốn cách chọn Áp dụng quy tắc nhân ta có 4.4=16 số tự nhiên cần tìm. Chọn A Câu 13: Gieo 3 đồng xu cân đối đồng chất mô tả không gian mẫu của phép thử: A. {NNN, SSS, NNS, SSN, NSN, SNS, NSS, SNN}. B. {NNN, SSS, NNS, SSN, NSN, SNS}. C. {NN, NS, SN, SS}. D. {NNN, SSS, NNS, SSN, NSN, NSS, SNN}. Phương pháp Áp dụng Một đồng xu có hai mặt, mỗi lần gieo như vậy có hai khả năng xuất hiện hoặc sấp, hoặc ngửa. Lời giải Một đồng xu có hai mặt, mỗi lần gieo như vậy có hai khả năng xuất hiện hoặc sấp, hoặc ngửa. Chọn A Câu 14: Rút ra hai lá bài từ cỗ bài tú lơ khơ 52 lá. Xác suất để rút được ít nhất một lá ách (A) là bao nhiêu? A. \(\frac{{33}}{{221}}\). B. \(\frac{{32}}{{221}}\). C. \(\frac{1}{{221}}\). D. \(\frac{1}{{1326}}\). Phương pháp Công thức tính xác suất Lời giải: Số cách rút ra hai lá bài trong cỗ bài tú lơ khơ 52 lá là \(C_{52}^2 = 1326\) Gọi A là biến cố rút ra hai lá được ít nhất một lá ách Số phần tử của biến cố là: \(4.C_{48}^1 + C_4^2 = 192 + 6 = 198\) Xác suất của biến cố A là \(P = \frac{{n(A)}}{{n(\Omega )}} = \frac{{198}}{{1326}} = \frac{{33}}{{221}}\) Chọn A Câu 15: Gieo một con súc sắc cân đối đồng chất hai lần. Xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 10 bằng bao nhiêu? A. \(\frac{5}{6}\). B. \(\frac{1}{6}\). C. \(\frac{1}{{36}}\). D. \(\frac{7}{{36}}\). Phương pháp Công thức tính xác suất Lời giải: Gieo con súc sắc cân đối đồng chất hai lần số phần tử của không gian mẫu là \(n(\Omega ) = 36\). Gọi A là biến cố gieo con súc sắc mà tổng số chấm trong hai lần gieo nhỏ hơn 10. Suy ra \(\overline A \) là biến cố gieo con súc sắc mà tổng số chấm trong hai lần gieo không nhỏ hơn 10. Suy ra \(n\left( {\overline A } \right) = 1.1 + 1.2 + 1.3 = 6\) Vậy \(P(A) = 1 - \frac{6}{{36}} = \frac{5}{6}\) Chọn A Câu 16: Hàm số \(y = f(x)\)được gọi là đồng biến trên \((a;b)\)nếu: A. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\). B. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\). C. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) \le f({x_2})\). D. \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) \ge f({x_2})\). Phương pháp Dựa vào định nghĩa đồng biến của hàm số. Lời giải Chọn A \(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\) Câu 17: Hoành độ đỉnh của Parabol \(y = a{x^2} + bx + c\)\((a \ne 0)\)có công thức: A. \(\frac{{ - b}}{{2a}}\). B. \(\frac{b}{{2a}}\). C. \(\frac{{ - b}}{a}\). D. \(\frac{b}{a}\). Phương pháp Theo công thức tọa độ đỉnh của (P) Lời giải Chọn A Hoành độ đỉnh của Parabol \(y = a{x^2} + bx + c\)\((a \ne 0)\)có công thức: \(\frac{{ - b}}{{2a}}\). Câu 18: Bạn An giải phương trình \(\sqrt { - {x^2} + 2x + 4} = x - 2\) như sau: Bước 1: Bình phương 2 vế ta có PT hệ quả: \( - {x^2} + 2x + 4 = {(x - 2)^2}\) Bước 2: Thu gọn ta được PT: \( - 2{x^2} + 6x = 0\). Giải và tìm được \(x = 0\)hoặc \(x = 3\). Bước 3: Kết luận tập nghiệm của PT là \(S = \left\{ {0;3} \right\}\) Bài làm của bạn An đúng hay sai? A. Đúng. B. Sai từ Bước 1. C. Sai từ Bước 2. D. Sai từ Bước 3. Phương pháp Giải phương trình đưa được về phương trình bậc hai. Lời giải Khi biến đổi phương trình hệ quả hay bình phương hai vế ta cần thử lại nghiệm Chọn D Câu 19: Cho tam thức bậc hai \(f\left( x \right)\) có bảng xét dấu như sau
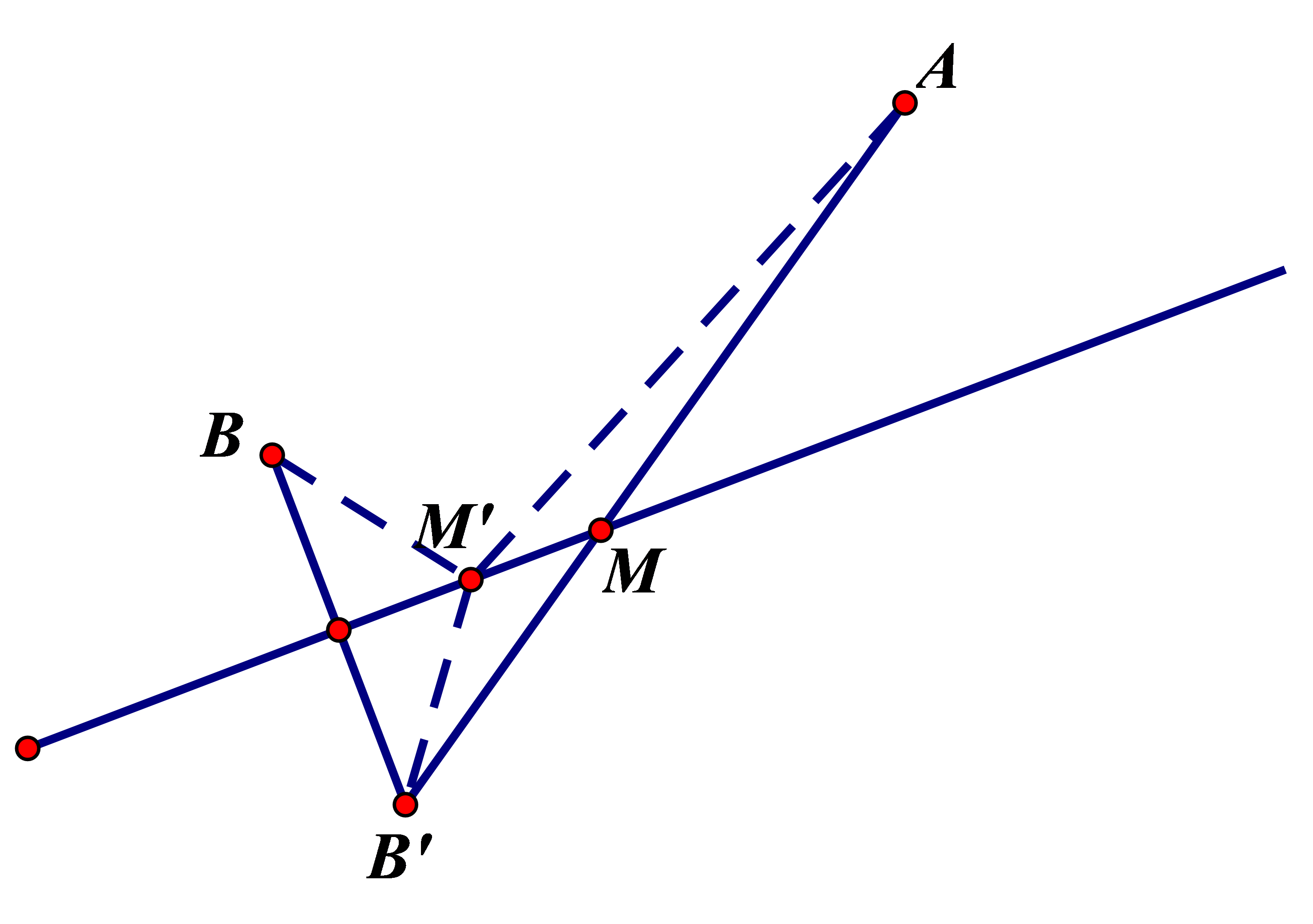
Mệnh đề nào dưới đây đúng? A. \(f\left( x \right) \ge 0\, \Leftrightarrow - 1 \le x \le 3.\) B. \(f\left( x \right) \ge 0\, \Leftrightarrow - 1 < x < 3.\) C. \(f\left( x \right) \ge 0\, \Leftrightarrow x > 3.\) D. \(f\left( x \right) \ge 0\, \Leftrightarrow x < - 1.\) Phương pháp Sử dụng quy tắc dấu của tam thức bậc hai Lời giải Chọn A \(f\left( x \right) \ge 0\, \Leftrightarrow - 1 \le x \le 3.\) Câu 20: Một véc tơ pháp tuyến của đường thẳng \(y = 3x - 2\) A. \(\overrightarrow n = (3;1)\). B. \(\overrightarrow n = (3; - 1)\). C. \(\overrightarrow n = (3; - 2)\). D. \(\overrightarrow n = (3;2)\). Phương pháp Vecto pháp tuyến của đường thẳng \(d:ax + by + c = 0\) là \(\overrightarrow n = \left( {a;b} \right)\) Lời giải \(y = 3x - 2 \Leftrightarrow 3x - y - 2 = 0\) Vậy vecto pháp tuyến của đường thẳng là \(\overrightarrow n (3; - 1)\) Chọn B Câu 21: Phương trình tham số của đường thẳng \(\Delta \) đi qua \(M({x_0};{y_0})\)và có Véc tơ chỉ phương \(\overrightarrow u = (a;b)\): A. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\). B. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} - bt}\end{array}} \right.\). C. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + bt}\\{y = {y_0} + at}\end{array}} \right.\) D. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} - bt}\\{y = {y_0} - at}\end{array}} \right.\). Phương pháp Theo định nghĩa phương trình tham số đường thẳng Lời giải Chọn A Phương trình tham số của đường thẳng \(\Delta \) đi qua \(M({x_0};{y_0})\)và có véc tơ chỉ phương \(\overrightarrow u = (a;b)\) là :\(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\) Câu 22: Có bao nhiêu vị trí tương đối giữa hai đường thẳng trong mặt phẳng? A. 1. B. 2. C. 3. D. 4. Phương pháp Sử dụng công thức vị trí tương đối của hai đường thẳng. Lời giải Chọn C Có 3 vị trí tương đối giữa hai đường thẳng trong mặt phẳng Câu 23: Trong mặt phẳng tọa độ \(Oxy\),Elip \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\)có độ dài tiêu cự: A. \(2\sqrt {{a^2} - {b^2}} \). B. \(\sqrt {2{a^2} - {b^2}} \). C. \(\sqrt {{a^2} - {b^2}} \). D. \(\sqrt {2{a^2} - 2{b^2}} \). Phương pháp Trong mặt phẳng tọa độ \(Oxy\),Elip \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\)có độ dài tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \) Lời giải Độ dài tiêu cự \(2c = 2\sqrt {{a^2} - {b^2}} \) Chọn A Câu 24: Xác định công thức đúng. A. \(A_n^k = \frac{{n!}}{{(n - k)!}}\). B. \(A_n^k = \frac{{n!}}{{(n - k)!k!}}\). C. \(A_n^k = \frac{{k!}}{{(n - k)!k!}}\). D. \(A_n^k = \frac{{k!}}{{(n - k)!n!}}\) Phương pháp Theo định nghĩa chỉnh hợp Lời giải Chọn A \(A_n^k = \frac{{n!}}{{(n - k)!}}\) Câu 25: Số tập hợp con của tập hợp có \(n\)phần tử A. \({2^n}\). B. \(2n\). C. \({3^n}\). D. \(3n\). Phương pháp Áp dụng quy tắc đếm Lời giải Chọn A.\({2^n}\) Câu 26: Có bao nhiêu cách sắp xếp 3 bạn vào một ghế dài 3 chỗ ngồi. A. 6. B. 12. C. 9. D. 27. Phương pháp Áp dụng công thức hoán vị Lời giải Xếp bạn vào một ghế dài có 3!=6 cách xếp Chọn A Câu 27: Minh có 3 cái áo sơ mi và 5 cái quần. Số cách để minh phối một bộ đồ (gồm 1 áo và 1 quần) là: A. 8. B. 15. C. 2. D. 45. Phương pháp Áp dụng quy tắc nhân Lời giải Chọn 1 cái áo trong 3 áo có 3 cách chọn Chọn 1 cái quần trong 5 quần có 5 cách chọn Áp dụng quy tắc nhân ta có 3.5=15 cách chọn một bộ quần áo. Chọn B Câu 28: Gieo 1 con súc sắc 2 lần thì có thể có bao nhiêu kết quả xảy ra? A. 36. B. 12. C. 6. D. 4. Phương pháp Áp dụng quy tắc nhân Lời giải Một lần gieo con súc sắc có 6 khả năng xảy ra Nên gieo hai lần có 6.6=36 kết quả xảy ra Chọn A Câu 29: Hệ số trong khai triển \({(a + b)^4}\)là: A. 1;4;6;4;1. B. 1;3;3;1. C. 1;5;10;10;5;1. D. 1;2;4;2;1. Phương pháp Sử dụng công thức khai triển nhị thức Newton Lời giải Ta có \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\) Chọn A Câu 30: Tìm tâm và bán kính của đường tròn có phương trình \({x^2} + {y^2} - 2x - 2y + 1 = 0\). A. \(I(1;1);\,\,R = 1.\) B. \(I( - 1; - 1);\,\,R = 1.\) C. \(I(1;1);\,\,R = 3.\) D. \(I( - 1; - 1);\,\,R = - 1.\) Phương pháp Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\) Lời giải Tâm \(I(1;1)\), bán kính \(R = \sqrt {{{( - 1)}^2} + {{( - 1)}^2} - 1} = 1\). Chọn A Câu 31: Trong các phương trình sau phương trình nào là phương trình đường tròn A. \({x^2} + {y^2} + 2x + 2y - 3 = 0\). B. \({x^2} + {y^2} + 2x + 2y + 3 = 0\). C. \(2{x^2} + {y^2} + 2x + 2y - 3 = 0\). D. \({x^2} - {y^2} + 2x + 2y - 3 = 0\). Phương pháp Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\) Lời giải Đáp án A \({( - 1)^2} + {( - 1)^2} + 3 > 0\) Đáp án C và D không phải là phương trình đường tròn vì hệ số của \({x^2};\,\,\,{y^2}\) khác nhau. Đáp B không phải là phương trình đường tròn vì \({( - 1)^2} + {( - 1)^2} - 3 < 0\) Chọn A Câu 32: Một hộp chứa 5 viên bi xanh, 4 viên bi đỏ. Lấy ra hai viên bi. Tính xác suất để hai viên bi được lấy ra là hai bi đỏ. A. \(\frac{1}{6}\). B. \(\frac{4}{9}\). C. \(\frac{5}{9}\). D. \(\frac{5}{{18}}\). Phương pháp Công thức tính xác suất Lời giải Số phần tử của không gian mẫu là \(n(\Omega ) = C_9^2\) Gọi A là biến cố lấy ra hai bi đều màu đỏ, số phần tử của biến cố A là \(n(A) = C_4^2\) Xác suất của biến cố A là \(P = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_4^2}}{{C_9^2}} = \frac{1}{6}\) Chọn A Câu 33: Có bao nhiêu cách xếp 10 người vào một bàn tròn A. 10!. B. 9! C. 8!. D. 11! Phương pháp Áp dụng công thức hoán vị Lời giải Vì đây là bàn tròn nên ta không phân biệt đâu là chỗ ngồi đầu Xếp người đầu tiên vào một chỗ để làm mốc Xếp 9 người còn lại vào 9 chỗ ngồi ta có 9! Cách xếp Chọn B Câu 34: Trong thùng xăm có 25 xăm tốt, 15 xăm xấu; anh An rút một xăm. Tính xác suất để anh An rút được xăm tốt. A. \(\frac{5}{8}\). B. \(\frac{3}{8}\). C. \(\frac{8}{5}\). D. \(\frac{8}{3}\). Phương pháp Công thức tính xác suất Lời giải Số phần tử của không gian mẫu là \(n(\Omega ) = 40\). Gọi A là biến cố rút ra được xăm tốt, số phần tử của biến cố A là \(n(A) = 25\) Xác suất của biến cố A là \(P = \frac{{n(A)}}{{n(\Omega )}} = \frac{{25}}{{40}} = \frac{5}{8}\) Chọn A Câu 35: Trong mặt phẳng \(Oxy,\) cho hai đường thẳng \({d_1}:\, - x + y + 1 = 0\) và \({d_2}:2\,x + 2y - 3 = 0.\) Góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) bằng A. \(45^\circ .\) B. \(60^\circ .\) C. \(90^\circ .\) D. \(30^\circ .\) Phương pháp Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {a,b} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\). Lời giải Ta có vectơ pháp tuyến của \({d_1}\); \({d_2}\) lần lượt là\(\overrightarrow n ( - 1;1);\,\,\overrightarrow {n'} (2;2)\) Ta có \(\overrightarrow n .\,\,\overrightarrow {n'} = - 1.2 + 1.2 = 0\) Suy ra \({d_1} \bot {d_2}\) hay góc giữa hai đường thẳng bằng \({90^0}\) Chọn C II. TỰ LUẬN(4câu - 3,0 điểm). Câu 36: Giải phương trình sau \(\sqrt {2x + 2\sqrt {2x - 1} } = x + 1\) Phương pháp Bình phương hai vế của phương trình để đưa về dạng phương trình bậc hai Lời giải Điều kiện: \(x \ge \frac{1}{2}\) \(\sqrt {2x + 2\sqrt {2x - 1} } = x + 1\) \(\begin{array}{l} \Leftrightarrow \sqrt {{{(\sqrt {2x - 1} + 1)}^2}} = x + 1 \Leftrightarrow \sqrt {2x - 1} = x\\ \Leftrightarrow 2x - 1 = {x^2} \Leftrightarrow {x^2} - 2x + 1 = 0 \Leftrightarrow x = 1\end{array}\) Vậy tập nghiệm của phương trình là \(S = \{ 1\} \) Câu 37: Trong mặt phẳng \(Oxy,\) cho điểm \(A\left( {1;\,2} \right),\,B( - 1;1)\)và đường thẳng \(d:x - y + 3 = 0\). Tìm tọa độ điểm \(M \in d\) để \(AM + BM\) nhỏ nhất. Phương pháp Vẽ hình Lời giải Đặt \(f(x,y) = x - y + 3\) Vì \(f(1;2).f( - 1;1) > 0\) nên hai điểm \(A,\,B\)nằm về cùng một nửa mặt phẳng bờ là đường thẳng d. Gọi \(B'\) đối xứng với \(B\) qua d suy ra tọa độ của \(B'\)(2; 2) Suy ra \(AM + BM = AM + B'M \ge AB'\) Nên \(AM + BM\) nhỏ nhất khi \(A,\,M,\,B'\)thẳng hàng hay M là giao điểm của \(d\,\)và \(AB'\) Suy ra M có tọa độ là \(( - 1;\,2)\). Câu 38: Trong mặt phẳng \(Oxy,\) cho tam giác \(ABC\) có \(A(2;1)\). Đường cao đi qua \(B\) có phương trình \(x - 3y - 7 = 0\), đường trung tuyến qua đỉnh \(C\)có phương trình \(x + y + 1 = 0\). Xác định tọa độ điểm \(B,\,C\). Phương pháp Toa độ C là giao điểm của đương thẳng AC và đường trung tuyến đi qua đỉnh C. Tọa độ B tìm thông qua trung điểm I của đoạn thẳng AB. Lời giải Phương trình đường thẳng AC có dạng \(3x + y - 7 = 0\) Tọa độ C là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y + 1 = 0\\3x + y - 7 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = - 5\end{array} \right.\) Gọi \(I(a; - a - 1)\) là tọa độ trung điểm của AB Suy ra tọa độ \(B(2a - 2; - 2a - 1)\) hay \(2a - 2 + 6a + 3 - 7 = 0 \Leftrightarrow a = \frac{3}{4}\) \( \Rightarrow B\left( {\frac{{ - 1}}{2};\frac{{ - 5}}{2}} \right)\). Câu 39: Tìm \(m\) để \(f(x) = ({m^2} - 1){x^2} + (m - 1)x - 2m - 1 < 0,\,\,\forall x \in \mathbb{R}\). Phương pháp Sử dụng dấu của tam thức bậc hai Lời giải TH 1: \({m^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\) Khi \(m = 1\) thì \(f(x) = - 2.1 - 1 = - 3 < 0,\,\,\forall x \in \mathbb{R}\) Khi \(m = - 1\) thì \(f(x) = - 2.x + 1 < 0 \Leftrightarrow x > \frac{1}{2}\) TH 2: \({m^2} - 1 \ne 0 \Leftrightarrow \left[ \begin{array}{l}m \ne 1\\m \ne - 1\end{array} \right.\) \(\begin{array}{l}f(x) = ({m^2} - 1){x^2} + (m - 1)x - 2m - 1 < 0,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 1 < 0\\\Delta = {(m - 1)^2} - 4.({m^2} - 1)( - 2m - 1) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 < m < 1\\m - 1 + 8{m^2} + 4m + 8m + 4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 < m < 1\\8{m^2} + 13m + 3 < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 < m < 1\\\frac{{ - 13 - \sqrt {73} }}{{16}} < m < \frac{{ - 13 + \sqrt {73} }}{{16}}\end{array} \right. \Leftrightarrow - 1 < m < \frac{{ - 13 + \sqrt {73} }}{{16}}\end{array}\) Vậy \(m \in \left( { - 1;\frac{{ - 13 + \sqrt {73} }}{{16}}} \right) \cup \left\{ 1 \right\}\) thì \(f(x) = ({m^2} - 1){x^2} + (m - 1)x - 2m - 1 < 0,\,\,\forall x \in \mathbb{R}\). ………. HẾT……….
|