Đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 3Tải về Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 5 \) không là số nguyên” A. \(\sqrt 5 = \mathbb{Z}\) B. \(\sqrt 5 \in \mathbb{Z}\) C. \(\sqrt 5 \subset \mathbb{Z}\) D. \(\sqrt 5 \notin \mathbb{Z}\) Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
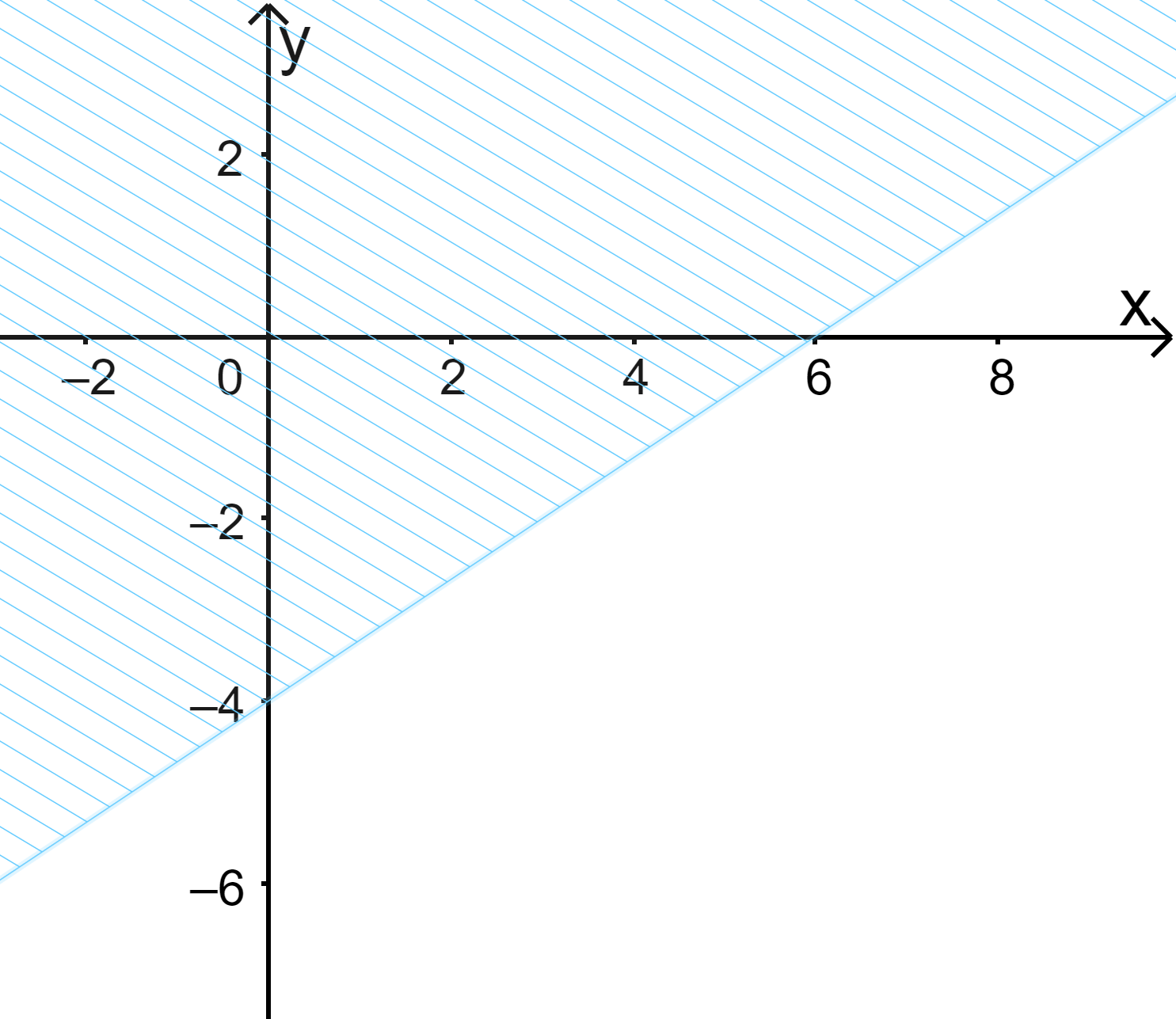
Đề bài I. PHẦN TRẮC NGHIỆM Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 5 \) không là số nguyên” A. \(\sqrt 5 = \mathbb{Z}\) B. \(\sqrt 5 \in \mathbb{Z}\) C. \(\sqrt 5 \subset \mathbb{Z}\) D. \(\sqrt 5 \notin \mathbb{Z}\) Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng? A. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\). B. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\). C. \(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\). D. \(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\) Câu 3. Cho \(A = \{ n = 2k|k \in \mathbb{N},k \le 3\} \) , \(B = \{ n \in \mathbb{N}|n \le 5\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 6\} \). Tìm tập hợp \(A{\rm{\backslash }}\left( {B \cup C} \right)\) A. \(\{ 0;8\} \) B. \(\{ 0\} \). C. \(\{ 8\} \). D. \(\emptyset \). Câu 4. Cho \(A = ( - 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A{\rm{\backslash }}B\) chứa đúng 5 số nguyên là: A. \(1\). B. \(3\). C. \(5\) D. \(7\) Câu 5. Lớp 10A có 45 học sinh trong đó có 23 em thích môn Văn, 20 em thích môn Toán, 12 em không thích môn nào. Số em thích cả hai môn trên là : A. \(8\). B. \(10\). C. \(12\). D. \(14\). Câu 6. Miền nghiệm của bất phương trình \(2x + 3y \le 12\) là: A. C. Câu 7. Giá trị lớn nhất của \(F(x;y) = 5x - 3y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\) A.\( - 2\) B. \(10\) C.\(\frac{{10}}{3}\) D. \( - 15\) Câu 8. Cho góc \(x\;({0^ \circ } < x < {180^ \circ })\) thỏa mãn \(\tan x = 5\). Tính biểu thức \(P = \frac{{3\sin x + 11\cos x}}{{7\sin x - 9\cos x}}\) A. \(\frac{{ - 29}}{{19}}\). B. \(\frac{{29}}{{19}}\). C. \( - 1\). D. \(1\). Câu 9. Rút gọn biểu thức \(A = \frac{{\sin x + \sin 3x + \sin 5x}}{{\cos x + \cos 3x + \cos 5x}}\) A.\(\sin 3x\) B. \(\cos 3x\). C. \(\tan 3x\). D. \(\tan x\). Câu 10. Cho tam giác ABC. Mệnh đề nào sau đây đúng? A. \(\sin (A + B) = - \sin C\) B. \(\sin \left( {\frac{{A + B}}{2}} \right) = \cos \frac{C}{2}\) C. \(\cos (A + B) = \cos C\) D. \(\tan (A + B) = \tan C\) Câu 11. Cho tam giác ABC có \(BC = 5,\widehat {BAC} = {120^o}\). Bán kính đường tròn ngoại tiếp \(\Delta ABC\) bằng: A.\(R = \frac{{5\sqrt 3 }}{2}\) B. \(R = \frac{5}{2}\) C. \(R = \frac{{5\sqrt 3 }}{3}\) D. \(R = 5\) Câu 12. Cho tam giác \(ABC\) có \(c = 4,b = 7,\widehat A = {60^ \circ }\). Chiều cao \({h_a}\) của tam giác ABC (làm tròn đến hàng đơn vị) là: A. \(2\) B. \(3\) C. \(4\) D. \(5\) Câu 13. Điểm \(A(2;3)\) thuộc miền nghiệm của hệ bất phương trình nào dưới đây? A. \(\left\{ \begin{array}{l}x + 2y > 9\\3x - y < 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}2x - y > 7\\x + y \le 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x + 5 \le 10\\4x - y > 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x + 5y > 8\\x - 3y \le 4\end{array} \right.\) Câu 14. Đơn giản biểu thức \(A = \sin \left( {\frac{{5\pi }}{2} - x} \right) + \cos \left( {13\pi + x} \right) - 3\sin \left( {x - 5\pi } \right)\) A. \(3\sin x\) B. \(3\sin x - \cos x\) C. \( - 3\sin x\). D. \(2\cos x + 3\sin x\). Câu 15. Cho bất phương trình \(5(2x - 3y) - 3(2x - y + 7) > x - 3y\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho? A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; - 2)\). D. \(C(0;2)\) II. PHẦN TỰ LUẬN Câu 1. Xác định các tập hợp sau và biểu diễn chúng trên trục số. a) \(( - \infty ;1) \cap ( - 5; + \infty )\) b) \((2;6] \cup ( - 3;5]\) c) \([ - 3;7){\rm{\backslash }}(4; + \infty )\) d) \(\mathbb{R}{\rm{\backslash }}( - 4;9]\) Câu 2. Một xưởng nhỏ sản xuất hai loại sản phẩm A và B, mỗi cân sản phẩm loại A cần 2 cân nguyên liệu và 30 giờ sản xuất, mức lợi nhuận đem lại là 400 nghìn đồng/kg. Một cân sản phẩm loại B cần 4 cân nuyên liệu và 15 giờ sản xuất, mức lợi nhuận đem lại là 300 nghìn đồng. Mỗi ngày xưởng có 200 cân nguyên liệu và 1200 giờ làm việc. Vậy mỗi ngày xưởng đó nên sản xuất mỗi loại sản phẩm bao nhiêu kg để thu về mức lợi nhuận cao nhất? Câu 3. Chứng minh rằng trong mọi tam giác ABC ta có: a) \(a = b.\cos C + c.\cos B\) b) \({m_a}^2 + {m_b}^2 + {m_c}^2 = \frac{3}{4}({a^2} + {b^2} + {c^2})\) Câu 4. Chứng minh trong mọi tam giác ABC ta đều có \(\frac{1}{r} = \frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}}\) Lời giải chi tiết I. PHẦN TRẮC NGHIỆM
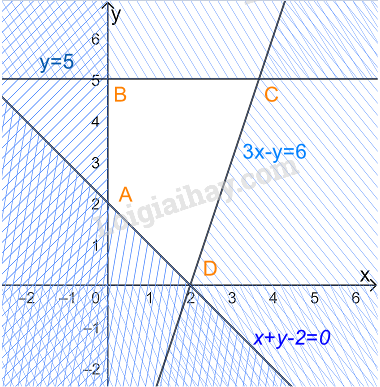
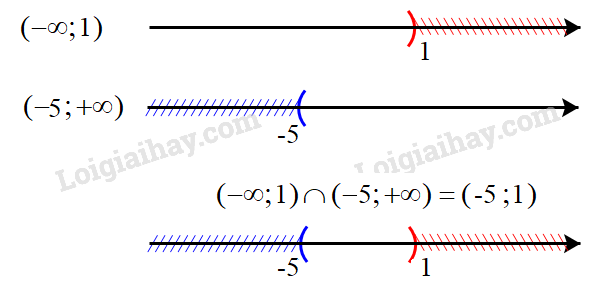
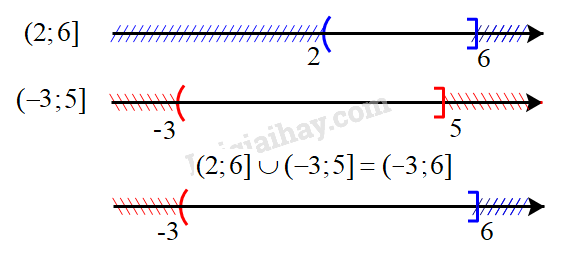
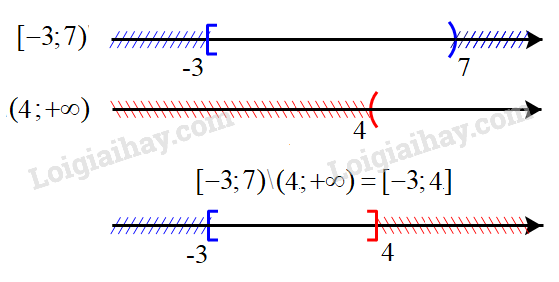
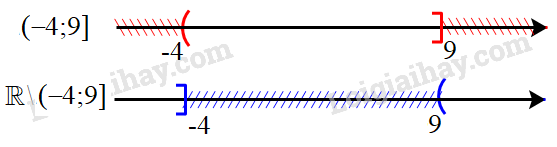
Câu 1: Cách giải: Tập hợp các số nguyên: \(\mathbb{Z}\) “\(\sqrt 5 \) không là số nguyên” viết là: \(\sqrt 5 \notin \mathbb{Z}\) Chọn D. Câu 2: Cách giải: Mệnh đề “\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\)” sai, chẳng hạn \(x = - 3\) thì \({x^2} > 1\) nhưng \(x < - 1\) Mệnh đề “\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\)” sai, chẳng hạn \(x = - 3\) thì \({x^2} > 1\) nhưng \(x < 1\) Mệnh đề “\(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\)” sai, chẳng hạn \(x = 0 > - 1\) nhưng \({x^2} < 1\) Mệnh đề “\(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)” đúng Chọn D. Câu 3: Phương pháp: Liệt kê các phần tử của tập hợp A, B, C Cách giải: \(A = \{ 0;2;4;6;8\} \) \(B = \{ 0;1;2;3;4;5\} \) \(C = \{ 2;3;4;5;6\} \). Ta có: \(B \cup C = \{ 0;1;2;3;4;5;6\} \Rightarrow A{\rm{\backslash }}\left( {B \cup C} \right) = \{ 0;8\} \) Chọn D. Câu 4: Cách giải: + Nếu \(m \ge 5\) thì \(A{\rm{\backslash }}B = ( - 2;5]{\rm{\backslash }}(m; + \infty ) = A = ( - 2;5]\), chứa 7 số nguyên là -1 ; 0 ;1 ;2 ;3 ;4 ;5 (nhiều hơn 3) nên ta loại trường hợp m > 5. + Để \(A{\rm{\backslash }}B \ne \emptyset \) thì m>-2. Xét trường hợp -2<m<5, khi đó \(A{\rm{\backslash }}B = ( - 2;5]{\rm{\backslash }}(m; + \infty ) = ( - 2;m]\) Chứa 5 số nguyên \( - 1;0;1;2;3\) thì \(m = 3\). Chọn B. Câu 5: Cách giải: Gọi X là tập hợp học sinh lớp 10A A là tập hợp các học sinh thích môn Văn. B là là tập hợp các học sinh thích môn Toán. Suy ra : \(A \cap B\) là tập hợp các học sinh tham gia cả hai môn Văn và Toán. \(A \cup B\) là tập hợp các học sinh thích môn Văn và Toán. \(X{\rm{\backslash }}\left( {A \cup B} \right)\) là tập hợp các học sinh không thích môn nào. Ta có : \(n(A) = 23;n(B) = 20;n\left( {X{\rm{\backslash }}\left( {A \cup B} \right)} \right) = 12\) \( \Rightarrow \) Số học sinh thích môn Văn và Toán là: \(n\left( {A \cup B} \right) = 45 - 12 = 33\) (học sinh) \( \Rightarrow \) Số học sinh học sinh thích cả hai môn Văn và Toán là: \(n(A \cap B) = n(A) + n(B) - n(A \cup B) = 23 + 20 - 33 = 10\) (học sinh) Chọn B. Câu 6: Phương pháp: Xác định đường thẳng \(2x + 3y = 12\) và xét một điểm (không thuộc đường thẳng) xem có thuộc miền nghiệm hay không. Cách giải: Đường thẳng \(2x + 3y = 12\) đi qua điểm có tọa độ (6;0) và (0;4) => Loại A, D. Xét điểm O(0;0), ta có: \(2.0 + 3.0 = 0 < 12\) nên O thuộc miền nghiệm của BPT đã cho. Chọn C. Câu 7: Phương pháp: Bước 1: Biểu diễn miền nghiệm, xác định các đỉnh của miền nghiệm Bước 2: Thay tọa độ các đỉnh vào \(F(x;y) = 5x - 3y\), kết luận giá trị nhỏ nhất. Cách giải: Xét hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\) Biểu diễn miền nghiệm của hệ, ta được Miền nghiệm là miền tứ giác ABCD trong đó \(A\left( {0;2} \right),{\rm{ }}B\left( {0;5} \right),{\rm{ }}C\left( {\frac{{11}}{3};5} \right),D(2;0)\) Thay tọa độ các điểm A, B, C, D vào \(F(x;y) = 5x - 3y\) ta được \(F(0;2) = 5.0 - 3.2 = - 6\) \(F(0;5) = 5.0 - 3.5 = - 15\) \(F\left( {\frac{{11}}{3};5} \right) = 5.\frac{{11}}{3} - 3.5 = \frac{{10}}{3}\) \(F(2;0) = 5.2 - 3.0 = 10\) Vậy giá trị lớn nhất của F bằng 10. Chọn B. Câu 8: Phương pháp: Chia cả tử và mẫu của P cho cosx để làm xuất hiện tanx. Cách giải: Vì \(\tan x = 5\) nên \(\cos x \ne 0\) Khi đó: \(P = \frac{{3\sin x + 11\cos x}}{{7\sin x - 9\cos x}} = \frac{{\frac{{3\sin x + 11\cos x}}{{\cos x}}}}{{\frac{{7\sin x - 9\cos x}}{{\cos x}}}} = \frac{{3\frac{{\sin x}}{{\cos x}} + 11}}{{7\frac{{\sin x}}{{\cos x}} - 9}}\) \( = \frac{{3\tan x + 11}}{{7\tan x - 9}} = \frac{{3.5 + 11}}{{7.5 - 9}} = 1\) Chọn D. Câu 9: Phương pháp: Áp dụng công thức: \(\sin x + \sin 5x = 2\sin \frac{{x + 5x}}{2}\cos \frac{{x - 5x}}{2}\) \(\cos x + \cos 5x = 2\cos \frac{{x + 5x}}{2}\cos \frac{{x - 5x}}{2}\) Cách giải: Ta có: \(\sin x + \sin 5x = 2\sin \frac{{x + 5x}}{2}\cos \frac{{x - 5x}}{2} = 2\sin 3x\cos \left( { - 2x} \right)\) \(\cos x + \cos 5x = 2\cos \frac{{x + 5x}}{2}\cos \frac{{x - 5x}}{2} = 2\cos 3x\cos \left( { - 2x} \right)\) \( \Rightarrow A = \frac{{2\sin 3x\cos \left( { - 2x} \right) + \sin 3x}}{{2\cos 3x\cos \left( { - 2x} \right) + \cos 3x}} = \frac{{\sin 3x\left[ {2\cos \left( { - 2x} \right) + 1} \right]}}{{\cos 3x\left[ {2\cos \left( { - 2x} \right) + 1} \right]}} = \frac{{\sin 3x}}{{\cos 3x}} = \tan 3x\) Chọn C. Câu 10: Phương pháp \(\begin{array}{l}\sin \left( {{{180}^ \circ } - x} \right) = \sin x\\\cos \left( {{{180}^ \circ } - x} \right) = - \cos x\\\tan \left( {{{180}^ \circ } - x} \right) = - \tan x\\\sin \left( {{{90}^ \circ } - x} \right) = \cos x\end{array}\) Cách giải: Ta có: \(A + B + C = {180^ \circ } \Rightarrow \left\{ \begin{array}{l}A + B = {180^ \circ } - C\\\frac{{A + B}}{2} = {90^ \circ } - \frac{C}{2}\end{array} \right.\) Suy ra: \(\sin \left( {A + B} \right) = \sin \left( {{{180}^ \circ } - C} \right) = \sin C\) => Loại A \(\cos \left( {A + B} \right) = \cos \left( {{{180}^ \circ } - C} \right) = - \cos C\) => Loại B \(\tan \left( {A + B} \right) = \tan \left( {{{180}^ \circ } - C} \right) = - \tan C\) => Loại D \(\sin \left( {\frac{{A + B}}{2}} \right) = \sin \left( {{{90}^ \circ } - \frac{C}{2}} \right) = \cos \frac{C}{2}\) Chọn B. Câu 11: Phương pháp: Áp dụng định lí sin: \(\frac{a}{{\sin A}} = 2R\) Cách giải: Áp dụng định lí sin trong tam giác ABC, ta có: \(\frac{a}{{\sin A}} = 2R\) Mà \(a = BC = 5,\widehat {BAC} = {120^o}\) \( \Rightarrow R = \frac{a}{{2\sin A}} = \frac{5}{{2\sin {{120}^ \circ }}} = \frac{{5\sqrt 3 }}{3}\) Chọn C. Câu 12: Phương pháp: Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\) Cách giải: Ta có: \(c = 4,b = 7,\widehat A = {60^ \circ }\) Áp dụng định lí cosin trong tam giác ABC ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\) \(\begin{array}{l} \Leftrightarrow {a^2} = {7^2} + {4^2} - 2.7.4\cos {60^ \circ } = 37\\ \Rightarrow a = \sqrt {37} \end{array}\) Lại có: \(S = \frac{1}{2}b.c\sin A = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{b.c\sin A}}{a} = \frac{{7.4.\sin {{60}^ \circ }}}{{\sqrt {37} }} \approx 4\) Vậy độ dài đường cao \({h_a}\) là khoảng 4. Chọn C. Câu 13. Phương pháp: Thay tọa độ điểm A vào hệ BPT, hệ nào cho ta các mệnh đề đúng thì điểm A thuộc miền nghiệm của hệ BPT đó. Cách giải + Xét hệ \(\left\{ \begin{array}{l}x + 2y > 9\\3x - y < 5\end{array} \right.\), thay \(x = 2,y = 3\) ta được: \(2 + 2.3 = 8 > 9\) sai nên A(2;3) không thuộc miền nghiệm của hệ BPT. + Xét hệ \(\left\{ \begin{array}{l}2x - y > 7\\x + y \le 3\end{array} \right.\), thay \(x = 2,y = 3\) ta được: \(2.2 - 3 = 1 > 7\) sai nên A(2;3) không thuộc miền nghiệm của hệ BPT. + Xét hệ \(\left\{ \begin{array}{l}3x + 5 \le 10\\4x - y > 3\end{array} \right.\), thay \(x = 2,y = 3\) ta được: \(3.2 + 5 = 11 \le 10\) sai nên A(2;3) không thuộc miền nghiệm của hệ BPT. + Xét hệ \(\left\{ \begin{array}{l}2x + 5y > 8\\x - 3y \le 4\end{array} \right.\), thay \(x = 2,y = 3\) ta được: \(\left\{ \begin{array}{l}2.2 + 5.3 = 19 > 8\\2 - 3.3 = - 7 \le 4\end{array} \right.\) đúng nên A(2;3) thuộc miền nghiệm của hệ BPT. Chọn D. Câu 14. Cách giải Ta có: \(\sin \left( {\frac{{5\pi }}{2} - x} \right) = \sin \left( {2\pi + \frac{\pi }{2} - x} \right) = \sin \left( {\frac{\pi }{2} - x} \right) = \cos x\) \(\cos \left( {13\pi + x} \right) = \cos \left( {12\pi + x + \pi } \right) = \cos \left( {x + \pi } \right) = - \cos x\) \(\sin \left( {x - 5\pi } \right) = \sin \left( {x + \pi - 6\pi } \right) = \sin \left( {x + \pi } \right) = - \sin x\) \( \Rightarrow A = \cos x + \left( { - \cos x} \right) - 3\left( { - \sin x} \right) = 3\sin x\) Chọn A Câu 15. Cho bất phương trình \(5(2x - 3y) - 3(2x - y + 7) > x - 3y\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho? A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; - 2)\). D. \(C(0;2)\) Cách giải: Ta có: \(5(2x - 3y) - 3(2x - y + 7) > x - 3y\) \(\begin{array}{l} \Leftrightarrow 10x - 15y - 6x + 3y - 21 - x + 3y > 0\\ \Leftrightarrow 3x - 9y - 21 > 0\\ \Leftrightarrow x - 3y - 7 > 0\end{array}\) Thay tọa độ các điểm vào BPT: + Vì \(0 - 3.0 - 7 = - 7 < 0\) nên \(O(0;0)\) không thuộc miền nghiệm + Vì \(1 - 3.0 - 7 = - 6 < 0\) nên \(A(1;0)\) không thuộc miền nghiệm + Vì \(3 - 3.( - 2) - 7 = 2 > 0\) nên \(B(3; - 2)\) thuộc miền nghiệm + Vì \(0 - 3.2 - 7 = - 13 < 0\) nên \(C(0;2)\) không thuộc miền nghiệm Chọn C II. PHẦN TỰ LUẬN Câu 1 (TH): Phương pháp: a) \(A \cap B = \{ x \in A|x \in B\} \) b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \) c, d) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \) Cách giải: a) Biểu diễn hai tập \(( - \infty ;1)\) và \(( - 5; + \infty )\) trên trục số, ta được: Giao của hai tập hợp: \(( - \infty ;1) \cap ( - 5; + \infty ) = ( - 5;1)\) b) Biểu diễn hai tập \((2;6]\) và \(( - 3;5]\) trên trục số, ta được: Hợp của hai tập hợp: \((2;6] \cup ( - 3;5] = ( - 3;6]\) c) Biểu diễn hai tập \(( - 3;7]\) và \((4; + \infty )\) trên trục số, ta được: Hiệu của hai tập hợp: \([ - 3;7){\rm{\backslash }}(4; + \infty ) = [ - 3;4]\) d) Biểu diễn tập \(( - 4;9]\) trên trục số, ta được: Hiệu của hai tập hợp: \(\mathbb{R}{\rm{\backslash }}( - 4;9] = ( - \infty ; - 4] \cup (9; + \infty )\)
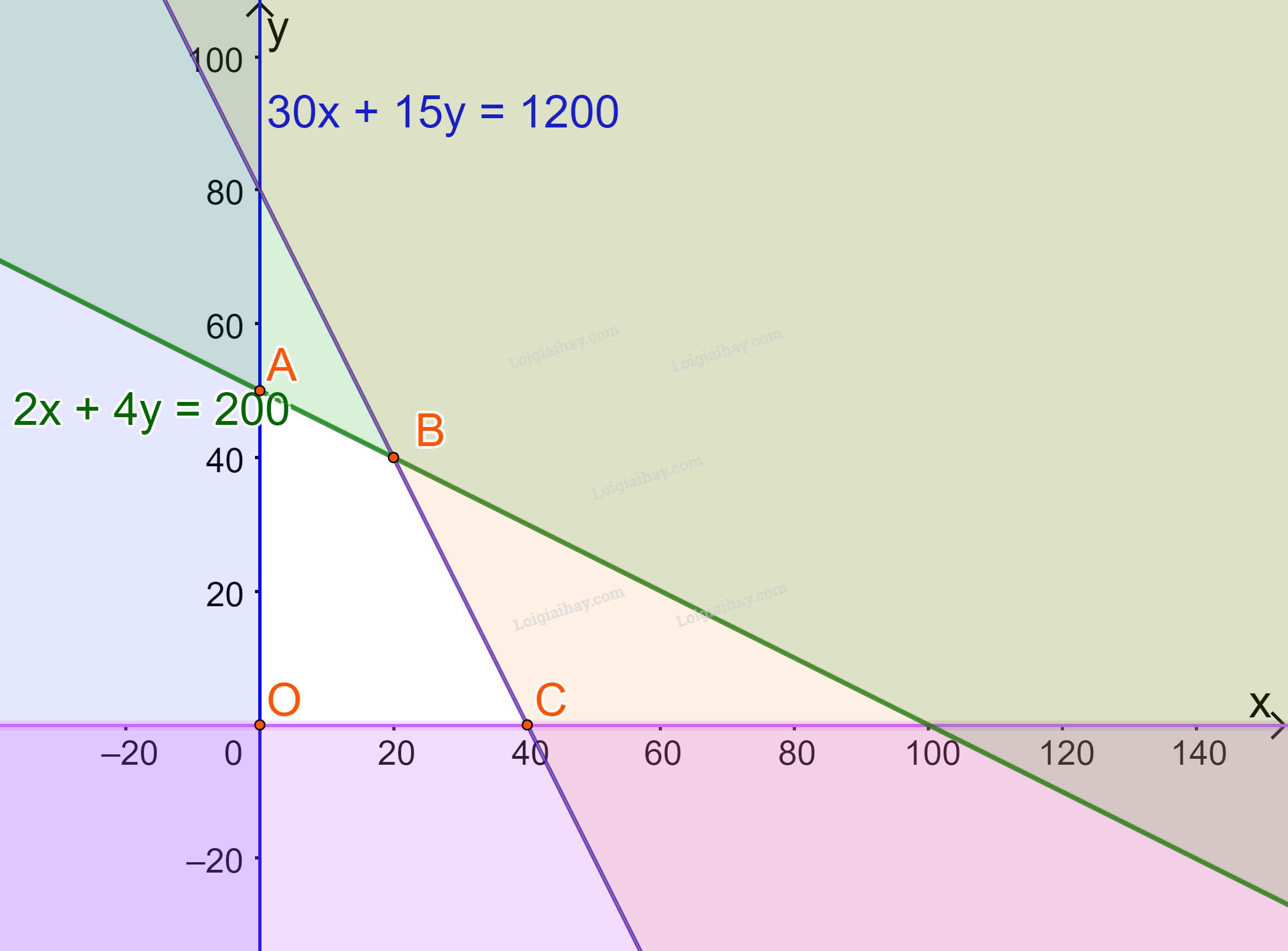
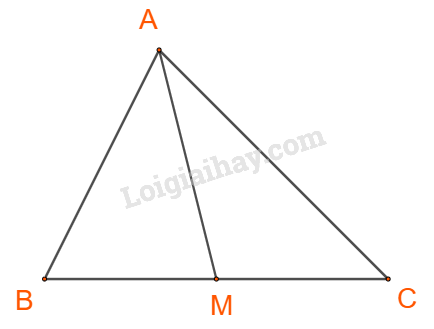
Câu 2: Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180? Cách giải: Gọi số kg sản phẩm loại A, loại B cần sản xuất mỗi ngày lần lượt là x, y \((x,y \ge 0)\) Để sản xuất x kg sản phẩm loại A cần 2x cân nguyên liệu và 30x giờ sản xuất, lợi nhuận đem lại là 400x nghìn đồng Để sản xuất y kg sản phẩm loại B cần 4y cân nguyên liệu và 15y giờ sản xuất, lợi nhuận đem lại là 300y nghìn đồng Mỗi ngày có 200 kg nguyên liệu nên \(2x + 4y \le 200\) Có 1200 giờ làm việc nên \(30x + 15y \le 1200\) Tổng lợi nhuận đem lại là: \(F(x;y) = 400x + 300y\) Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + 4y \le 200\\30x + 15y \le 1200\end{array} \right.\) Biểu diễn miền nghiệm trên hệ trục Oxy, ta được: Miền nghiệm là miền tứ giác OABC (kể cả các cạnh), trong đó \(A(0;50),B(20;40),C(40;0),O(0;0)\) Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 400x + 300y\) ta được: \(\begin{array}{l}F(0;0) = 400.0 + 300.0 = 0\\F(0;50) = 400.0 + 300.50 = 15000\\F(20;40) = 400.20 + 300.40 = 20000\\F(40;0) = 400.40 + 300.0 = 16000\end{array}\) Do đó F đạt giá trị lớn nhất bằng 15 000 (nghìn đồng) tại \(x = 20;y = 40\) Vậy mỗi ngày xưởng đó cần sản xuất 20kg sản phẩm loại A, 40kg sản phẩm loại B để thu về lợi nhuận lớn nhất. Câu 3: Phương pháp: a) Áp dụng hệ quả của định lí cosin: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\) b) Áp dụng các công thức tính diện tích:\(S = \frac{1}{2}a.{h_a} = \frac{{abc}}{{4R}}\) Định lí sin: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\) Cách giải: a) Từ định lí cosin, ta suy ra: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\) \(\begin{array}{l} \Rightarrow b\cos C + c.\cos B = b.\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} + c.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ = \frac{{{a^2} + {b^2} - {c^2}}}{{2a}} + \frac{{{a^2} + {c^2} - {b^2}}}{{2a}}\\ = \frac{{{a^2} + {b^2} - {c^2} + {a^2} + {c^2} - {b^2}}}{{2a}}\\ = \frac{{2{a^2}}}{{2a}} = a\\ = \frac{1}{2}\left( {2{b^2} - 2{c^2}} \right) = {b^2} - {c^2}\end{array}\) Vậy \(a = b.\cos C + c.\cos B\) b) Gọi M là trung điểm BC. Khi đó \(AM = {m_a}\) Áp dụng định lí cosin trong tam giác ABM, ta có: \(\begin{array}{l}A{M^2} = A{B^2} + B{M^2} - 2.AB.BM.\cos B\\ = {c^2} + {\left( {\frac{a}{2}} \right)^2} - 2.c.\frac{a}{2}.\cos B\\ = {c^2} + {\frac{a}{4}^2} - ac\cos B\end{array}\) Mà \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\), suy ra \({m_a}^2 = {c^2} + {\frac{a}{4}^2} - ac.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = {c^2} + {\frac{a}{4}^2} - \frac{{{a^2} + {c^2} - {b^2}}}{2} = \frac{{{c^2} + {b^2}}}{2} - {\frac{a}{4}^2}\) Tương tự ta có: \({m_b}^2 = \frac{{{c^2} + {a^2}}}{2} - {\frac{b}{4}^2};{m_c}^2 = \frac{{{b^2} + {a^2}}}{2} - {\frac{c}{4}^2}\) \(\begin{array}{l} \Rightarrow {m_a}^2 + {m_b}^2 + {m_c}^2 = \frac{{{c^2} + {b^2}}}{2} - {\frac{a}{4}^2} + \frac{{{c^2} + {a^2}}}{2} - {\frac{b}{4}^2} + \frac{{{b^2} + {a^2}}}{2} - {\frac{c}{4}^2}\\ = \frac{{{c^2}}}{2} + \frac{{{c^2}}}{2} - \frac{{{c^2}}}{4} + \frac{{{b^2}}}{2} + \frac{{{b^2}}}{2} - \frac{{{b^2}}}{4} + \frac{{{a^2}}}{2} + \frac{{{a^2}}}{2} - \frac{{{a^2}}}{4}\\ = \frac{{3{c^2}}}{4} + \frac{{3{b^2}}}{4} + \frac{{3{a^2}}}{4} = \frac{3}{4}({a^2} + {b^2} + {c^2})\end{array}\)
Ta được điều phải chứng minh.
Câu 4: Cách giải: Xét tam giác ABC có \(a = BC,b = AC,c = AB\) Ta có: \(S = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} \Rightarrow \frac{1}{{{h_a}}} = \frac{a}{{2S}}\) Tương tự ta có: \(\frac{1}{{{h_b}}} = \frac{b}{{2S}};\frac{1}{{{h_c}}} = \frac{c}{{2S}}\) \( \Rightarrow \frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{a}{{2S}} + \frac{b}{{2S}} + \frac{c}{{2S}} = \frac{{a + b + c}}{{2S}}\) Lại có: \(S = pr = \frac{{a + b + c}}{2}.r \Rightarrow r = \frac{{2S}}{{a + b + c}} \Rightarrow \frac{1}{r} = \frac{{a + b + c}}{{2S}}\) Do đó \(\frac{1}{r} = \frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}}\) (đpcm)
|













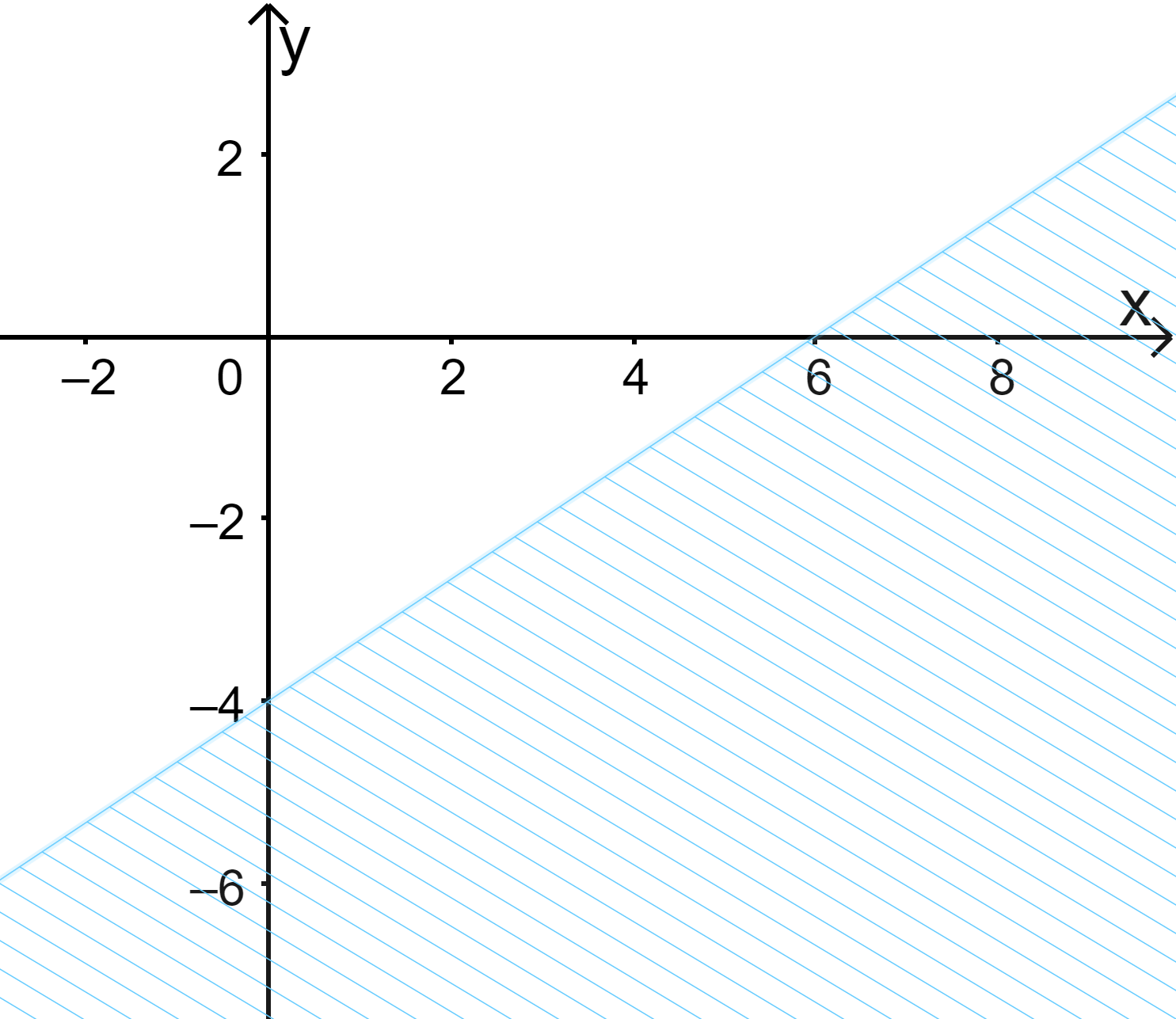 B.
B. 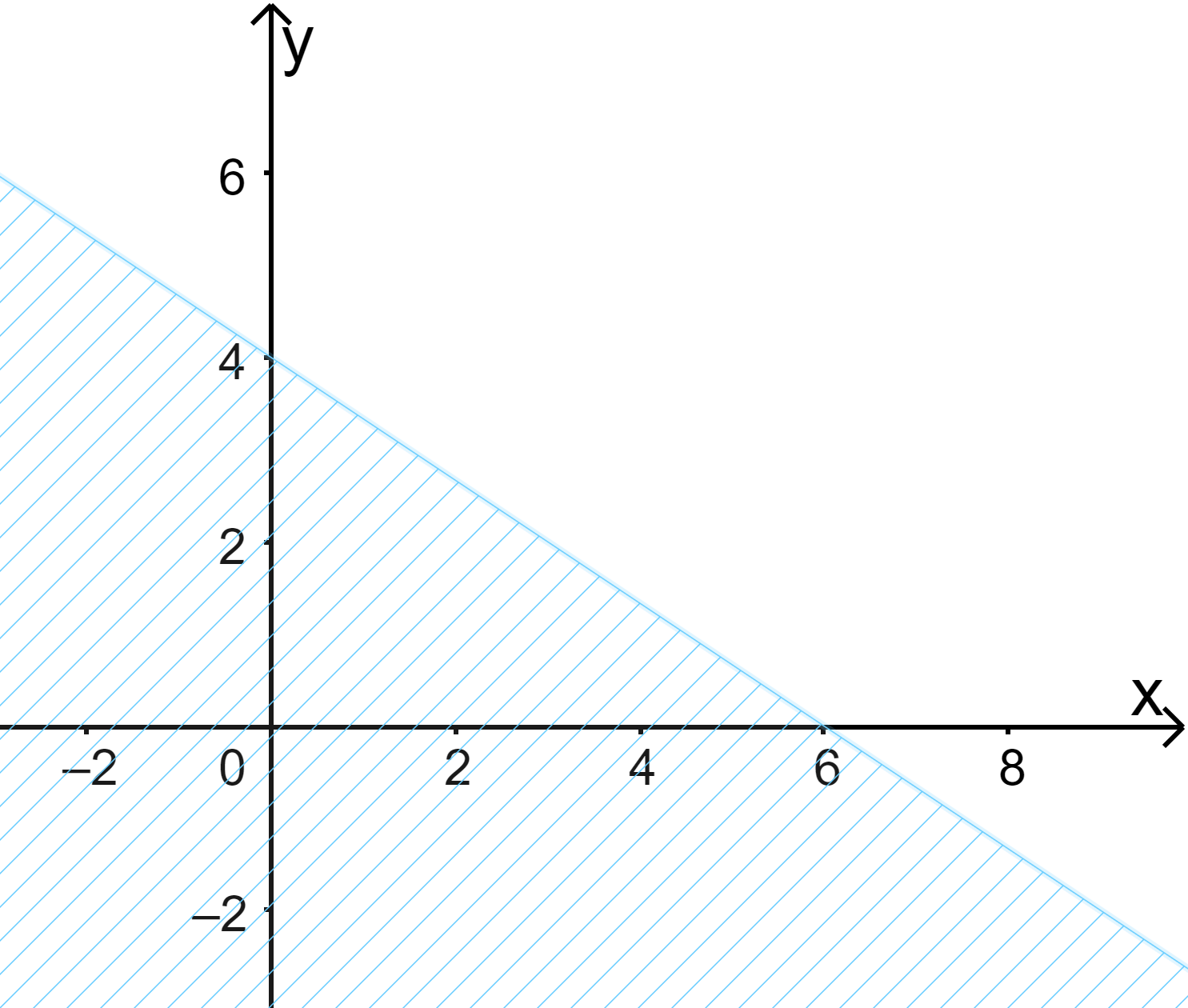
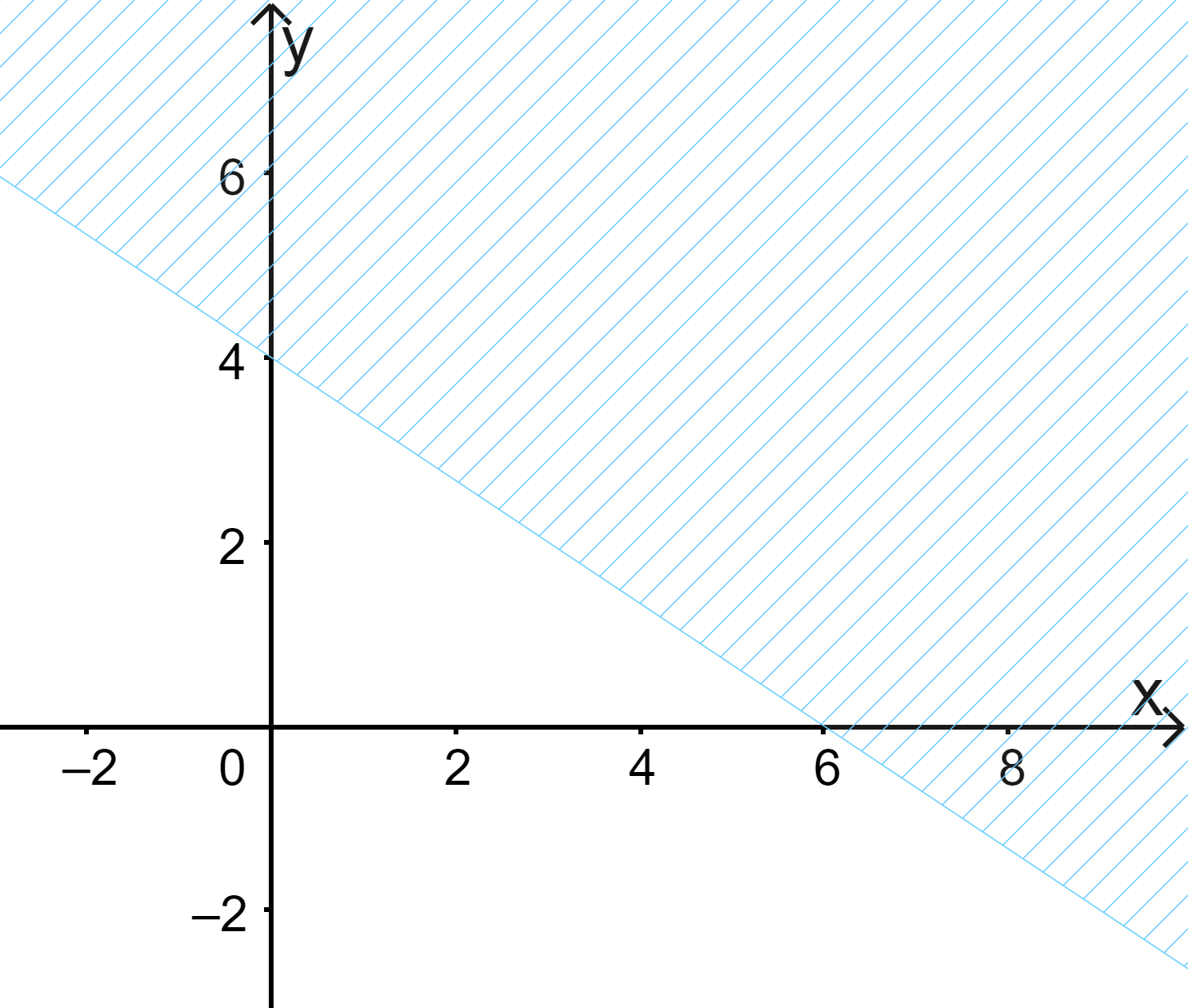 D.
D.