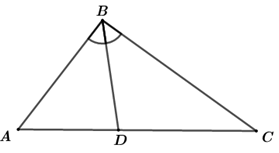
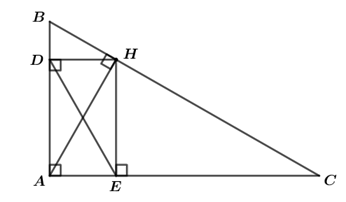
Đề kiểm tra giữa kì II Toán 8 - Đề số 5 có lời giải chi tiết

Đề bài

 Phần I: Trắc nghiệm (2,0 điểm) Ghi vào bài làm chữ cái đứng trước đáp án trả lời đúng ;

a) Điều kiện xác định của phương trình $\frac{x}{{3 - x}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x - 3} \right)}}$

A. $x \ne  - 2$ hoặc $x \ne 3$       B. $x \ne 2$ và $x \ne  - 3$

C. $x \ne 3$ và $x \ne  - 2$          D. $x \ne 0$ và $x \ne 3$

b) Số nghiệm của phương trình $\left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right)\left( {5x + 10} \right) = 0$ là:

A. Bốn nghiệm                   B. Ba nghiệm

C. Vô số nghiệm                D. Một nghiệm

c) $\Delta ABC$ đồng dạng với $\Delta MNP$ theo trường hợp cạnh – góc – cạnh nếu có:

A. $\angle B = \angle M;\,\,\frac{{CB}}{{MP}} = \frac{{AC}}{{NP}}$                   

B. $\angle A = \angle M;\,\,\angle B = \angle P$                            

C. $\angle A = \angle M;\,\,\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}}$        

D. $\angle A = \angle M;\,\,\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}$

d) Cho $\Delta ABC$, $BD$ là tia phân giác của góc $B\,\,\left( {D \in AC} \right)$, khi đó ta có:

A. $\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}}$           B. $\frac{{DA}}{{DC}} = \frac{{BD}}{{BC}}$      

C. $\frac{{DA}}{{DC}} = \frac{{BC}}{{BA}}$           D. $\frac{{DA}}{{DC}} = \frac{{BD}}{{BA}}$

Phần II: Tự luận (8,0 điểm)

Bài 1 : (2 điểm)  

Giải các phương trình sau:

a) $\frac{{2x}}{3} + \frac{{3x - 1}}{6} = \frac{x}{2}$

b) $3{x^2} - 3x = \left( {x - 1} \right)\left( {x + 3} \right)$

c) $\frac{{x - 2}}{{x + 2}} - \frac{3}{{x - 2}} = \frac{{2x - 22}}{{{x^2} - 4}}$

Bài 2:  (2 điểm)

Giải bài toán bằng cách lập phương trình:

Một tổ sản xuất dự định làm một số sản phẩm trong một thời gian nhất định. Tổ dự định mỗi ngày làm $120$ sản phẩm. Khi thực hiện, mỗi ngày tổ làm được $150$ sản phẩm. Vì vậy tổ đã làm xong trước thời gian dự định là $4$ ngày và còn làm thêm được $10$ sản phẩm nữa. Tính số sản phẩm mà tổ đã dự định làm ?

Bài 3: (3 điểm)

Cho $\Delta ABC$ vuông ở $A$, đường cao $AH$.

a) Chứng minh $\Delta AHB \sim \Delta CAB$ và $AH.CB = AB.AC$.

b) Gọi $D,\,\,E$ lần lượt là hình chiếu của $H$ lên $AB,\,\,AC$. Tứ giác $DHEA$ là hình gì? Vì sao?

c) Cho $AB = 9cm,\,\,AC = 12cm$. Tính $DE$?

d) Chứng minh rằng $A{H^2} = DA\,.\,DB + EA\,.\,EC$

Bài 4: (0,5 điểm)  Giải và biện luận phương trình sau theo tham số $m$:

$\frac{{x + 1}}{{x + 2 + m}} = \frac{{x - 1}}{{x + 2 - m}}$

Lời giải chi tiết

Phần I: Trắc nghiệm  

a). C

b). B

c). D

d). A

a) (NB):

Phương pháp:

Điều kiện để phân thức $\frac{A}{B}$ có nghĩa $\Leftrightarrow B \ne 0$

Cách giải:

Điều kiện xác định:

$\left\{ \begin{array}{l}3 - x \ne 0\\\left( {x + 2} \right)\left( {x - 3} \right) \ne 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}3 - x \ne 0\\x + 2 \ne 0\\x - 3 \ne 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x \ne 3\\x \ne  - 2\end{array} \right.$

Vậy $x \ne 3$ và $x \ne  - 2$.

Chọn C.

b) (TH):

Phương pháp:

Phương trình tích:

 ${A_1}\left( x \right).{A_2}\left( x \right) \ldots {A_n}\left( x \right) = 0$$\Leftrightarrow \left[ \begin{array}{l}{A_1}\left( x \right) = 0\\{A_2}\left( x \right) = 0\\...\\{A_n}\left( x \right) = 0\end{array} \right.$

Cách giải:

$\left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right)\left( {5x + 10} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\\x - 3 = 0\\5x + 10 = 0\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 2\\x = 3\\x =  - 2\end{array} \right.$  (thỏa mãn)

Tập nghiệm của phương trình là $S = \left\{ { - 2;\,\,1;\,\,3} \right\}$.

Vậy phương trình đã cho có $3$ nghiệm.

Chọn B.

c) (TH):

Phương pháp:

Áp dụng trường hợp đồng dạng thứ hai.

Nếu $\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}$ và $\angle A = \angle A'$ thì $\Delta ABC \sim \Delta A'B'C'\,\,\left( {c - g - c} \right)$

Cách giải:

$\Delta ABC$ đồng dạng với $\Delta MNP$ theo trường hợp cạnh – góc – cạnh nếu: $\angle A = \angle M;\,\,\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}$

Chọn D.

d) (NB):

Phương pháp:

 Áp dụng định lý về tính chất đường phân giác trong tam giác.

Cách giải:

                                                   

Xét tam giác $ABC$, có $BD$ là tia phân giác của $\angle ABC$$\,\left( {D \in AC} \right)$ .

Áp dụng định lý về tính chất đường phân giác trong tam giác ta có:  $\frac{{AB}}{{BC}} = \frac{{AD}}{{DC}}$

$\Rightarrow \frac{{DA}}{{DC}} = \frac{{BA}}{{BC}}$

Chọn A.

II. TỰ LUẬN

Bài  1 (VD):

Phương pháp:

a) Phương trình không chứa ẩn ở mẫu:

Đưa phương trình về dạng $ax + b = 0$ hay $ax =  - b$.

b) Đưa phương trình đã cho về dạng phương trình tích:

$A\left( x \right).B\left( x \right) = 0$$\Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.$

c) Phương trình chứa ẩn ở mẫu:

+ Tìm điều kiện xác định của phương trình.

+ Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

+ Giải phương trình vừa nhận được.

+ Kiểm tra và kết luận. Với những giá trị của ẩn tìm trong bước 3, các giá trị thỏa mãn được điều kiện xác định ở bước 1 chính là nghiệm của phương trình đã cho.

Cách giải:

Giải các phương trình sau:

a) $\frac{{2x}}{3} + \frac{{3x - 1}}{6} = \frac{x}{2}$

$\begin{array}{l}\frac{{2x}}{3} + \frac{{3x - 1}}{6} = \frac{x}{2}\\ \Leftrightarrow \frac{{4x}}{6} + \frac{{3x - 1}}{6} = \frac{{3x}}{6}\\ \Leftrightarrow \frac{{7x - 1}}{6} = \frac{{3x}}{6}\\ \Rightarrow 7x - 1 = 3x\\ \Leftrightarrow 7x - 3x = 1\\ \Leftrightarrow 4x = 1\\ \Leftrightarrow x = \frac{1}{4}\end{array}$

Vậy tập nghiệm của phương trình là $S = \left\{ {\frac{1}{4}} \right\}$.

b) $3{x^2} - 3x = \left( {x - 1} \right)\left( {x + 3} \right)$

$\begin{array}{l}3{x^2} - 3x = \left( {x - 1} \right)\left( {x + 3} \right)\\ \Leftrightarrow 3{x^2} - 3x - \left( {x - 1} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow 3x\left( {x - 1} \right) - \left( {x - 1} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left[ {3x - \left( {x + 3} \right)} \right] = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {3x - x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {2x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2}\\x = 1\end{array} \right.\end{array}$

Vậy $S = \left\{ {\frac{3}{2};\,\,1} \right\}$.

c) $\frac{{x - 2}}{{x + 2}} - \frac{3}{{x - 2}} = \frac{{2x - 22}}{{{x^2} - 4}}$

     $\frac{{x - 2}}{{x + 2}} - \frac{3}{{x - 2}} = \frac{{2x - 22}}{{{x^2} - 4}}$                                                                   

Điều kiện: $\left\{ \begin{array}{l}x + 2 \ne 0\\x - 2 \ne 0\\{x^2} - 4 \ne 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x \ne  - 2\\x \ne 2\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \frac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} - \frac{{3\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \frac{{2x - 22}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\\ \Rightarrow {\left( {x - 2} \right)^2} - 3\left( {x + 2} \right) = 2x - 22\\ \Leftrightarrow {x^2} - 4x + 4 - 3x - 6 = 2x - 22\\ \Leftrightarrow {x^2} - 4x + 4 - 3x - 6 - 2x + 22 = 0\\ \Leftrightarrow {x^2} - 9x + 20 = 0\\ \Leftrightarrow {x^2} - 4x - 5x + 20 = 0\\ \Leftrightarrow x\left( {x - 4} \right) - 5\left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\x - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\,\,\,\left( {tm} \right)\\x = 5\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy tập  nghiệm của phương trình là $S = \left\{ {4;\,\,5} \right\}$.

Bài 2 (VD):

Phương pháp:

Các bước giải bài toán bằng cách lập phương trình:

Gọi số sản phẩm mà tổ đã dự định làm là $x$ (sản phẩm, $x \in {\mathbb{N}^*}$).

Thời gian tổ hoàn thành công việc theo dự định là $\frac{x}{{120}}$ (ngày).

Theo thực tế, số sản phẩm mà tổ làm được là $x + 10$ (sản phẩm).

Thời gian tổ hoàn thành công việc theo thực tế là $\frac{{x + 10}}{{150}}$ (ngày).

Dựa vào giả thiết bài cho để lập phương trình. Giải phương trình tìm ẩn  $x.$

Đối chiếu với điều kiện rồi kết luận

Cách giải:

Giải bài toán bằng cách lập phương trình:

Gọi số sản phẩm mà tổ đã dự định làm là $x$ (sản phẩm, $x \in {\mathbb{N}^*}$).

Thời gian tổ hoàn thành công việc theo dự định là $\frac{x}{{120}}$ (ngày).

Theo thực tế, số sản phẩm mà tổ làm được là $x + 10$ (sản phẩm).

Thời gian tổ hoàn thành công việc theo thực tế là $\frac{{x + 10}}{{150}}$ (ngày).

Vì tổ đã làm xong trước thời gian dự định là $4$ ngày nên ta có phương trình:

$\begin{array}{l}\,\,\,\,\frac{{x + 10}}{{150}} + 4 = \frac{x}{{120}}\\ \Leftrightarrow \frac{{4\left( {x + 10} \right)}}{{600}} + \frac{{2400}}{{600}} = \frac{{5x}}{{600}}\\ \Rightarrow 4\left( {x + 10} \right) + 2400 = 5x\\ \Leftrightarrow 4x + 40 + 2400 = 5x\\ \Leftrightarrow x = 2440\,\,\left( {tm} \right)\end{array}$

Vậy số sản phẩm mà tổ đã dự định làm là $2440$ sản phẩm.

Câu 3 (VD):

Phương pháp:

a) Áp dụng trường hợp đồng dạng thứ nhất (góc-góc).

b) Áp dụng dấu hiệu nhận biết hình chữ nhật (tứ giác có ba góc vuông).

c) Áp dụng tính chất của hình chữ nhật (hình chữ nhật có hai đường chéo bằng nhau).

Từ câu a) ta tìm được $AH$ và từ đó suy ra $DE$.

d) Chứng minh: $D{H^2} = DB.DA$, $E{H^2} = EC.EA$.

Sau đó, áp dụng tính chất hình chữ nhật, định lý Py-ta-go để suy ra điều cần chứng minh.

Cách giải:

Cho $\Delta ABC$ vuông ở $A$, đường cao $AH$.

                                                    

a) Chứng minh $\Delta AHB \sim \Delta CAB$ và $AH.CB = AB.AC$.

 Xét $\Delta AHB$ và $\Delta CAB$ ta có:

$\angle AHB = \angle CAB\,\,\left( { = {{90}^0}} \right)$

$\angle C$ chung

$\Rightarrow \Delta AHB \sim \Delta CAB$ (góc - góc)

$\Rightarrow \frac{{AH}}{{CA}} = \frac{{AB}}{{CB}}$ (Tỷ số cặp cạnh tương ứng)

$\Rightarrow \frac{{AH}}{{AC}} = \frac{{AB}}{{BC}} \Rightarrow AH.BC = AB.AC$ (đpcm).

b) Gọi $D,\,\,E$ lần lượt là hình chiếu của $H$ lên $AB,\,\,AC$. Tứ giác $DHEA$ là hình gì? Vì sao?

Theo đề bài, ta có:

$\Delta ABC$ vuông tại $A$ $\Rightarrow \angle BAC = {90^0}$ hay $\angle DAE = {90^0}$

$HD \bot AB$ tại $D$$\Rightarrow \angle HDA = {90^0}$

$HE \bot AC$ tại $E$$\Rightarrow \angle HEA = {90^0}$

Xét tứ giác $DHEA$ có $\angle DAE = \angle HDA = \angle HEA = {90^0}$.

$\Rightarrow$ Tứ giác $DHEA$ là hình chữ nhật (dấu hiệu nhận biết)

c) Cho $AB = 9cm,\,\,AC = 12cm$. Tính $DE$.

Xét $\Delta ABC$ vuông tại $A$, áp dụng định lý Py-ta-go ta có:

$A{B^2} + A{C^2} = B{C^2}$

$\Rightarrow B{C^2} = {9^2} + {12^2} = 225$

$\Rightarrow BC = 15\left( {cm} \right)$

Theo câu $a)$ ta có:

$\begin{array}{l}AH.BC = AB.AC\\ \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{9.12}}{{15}} = 7,2\left( {cm} \right)\end{array}$

Vì $DHEA$ là hình chữ nhật nên $DE = AH$ (tính chất của hình chữ nhật).

Mà $AH = 7,2cm$ nên $DE = AH = 7,2cm$.

d) Chứng minh rằng $A{H^2} = DA\,.\,DB + EA\,.\,EC$.

Xét $\Delta BDH$ và $\Delta HDA$ có:

$\angle BDH = \angle HDA\,\,\left( { = {{90}^0}} \right)$

$\angle BHD = \angle HAD$ (cùng phụ với $\angle DHA$)

$\Rightarrow \Delta BDH \sim \Delta HDA$ (góc-góc)

$\Rightarrow \frac{{BD}}{{HD}} = \frac{{DH}}{{DA}}$ $\Rightarrow D{H^2} = DB.DA$

Xét $\Delta CEH$ và $\Delta HEA$ có:

$\angle CEH = \angle HEA\,\,\left( { = {{90}^0}} \right)$

$\angle CHE = \angle HAE$ (cùng phụ với $\angle EHA$)

$\Rightarrow \Delta CEH \sim \Delta HEA$ (góc-góc)

$\Rightarrow \frac{{CE}}{{HE}} = \frac{{EH}}{{EA}}$$\Rightarrow E{H^2} = EC.EA$

Vì $DHEA$ là hình chữ nhật nên $EH = AD$(tính chất của hình chữ nhật).

$\Rightarrow A{D^2} = E{H^2} = EC.EA$

Ta có:

$\left. \begin{array}{l}D{H^2} = DB.DA\\A{D^2} = EC.EA\end{array} \right\}$

$\Rightarrow D{H^2} + A{D^2} =$$BD.AD + EC.EA$                                          $\left( 1 \right)$

Mà $\Delta ADH$ vuông tại $D$, áp dụng định lý Py-ta-go ta có: $A{H^2} = D{H^2} + AD{}^2$  $\left( 2 \right)$ 

Từ $\left( 1 \right)$ và $\left( 2 \right)$ $\Rightarrow$$A{H^2} = EC.EA + BD.AD$( đpcm).

Câu 4 (VDC):

Phương pháp:

- Tìm điều kiện xác định.

- Đưa phương trình đã cho về dạng $ax + b = 0$ hay $ax =  - b$.

+ Nếu $a = 0$: Phương trình $ax + b = 0$ trở thành $0x + b = 0$, khi đó:

Trường hơp 1: Với $b = 0$ thì phương trình $ax + b = 0$ có nghiệm đúng với mọi $x \in \mathbb{R}$.

Trường hợp 2: Với $b \ne 0$ thì phương trình $ax + b = 0$ vô nghiệm.

+ Nếu $a \ne 0$: $ax + b = 0 \Leftrightarrow x =  - \frac{b}{a}$.

Do đó, phương trình có nghiệm duy nhất $ax + b = 0 \Leftrightarrow x =  - \frac{b}{a}$.

Kết hợp với điều kiện xác định để tìm $m$.

Cách giải:

Giải và biện luận phương trình sau theo tham số $m$:

$\frac{{x + 1}}{{x + 2 + m}} = \frac{{x - 1}}{{x + 2 - m}}$

Điều kiện: $x \ne  - 2 - m$; $x \ne  - 2 + m$

$\begin{array}{l}\,\,\,\,\,\,\frac{{x + 1}}{{x + 2 + m}} = \frac{{x - 1}}{{x + 2 - m}}\,\,\,\,\,\,\,\,\\ \Rightarrow \left( {x + 1} \right)\left( {x + 2 - m} \right) = \left( {x - 1} \right)\left( {x + 2 + m} \right)\\ \Leftrightarrow {x^2} + 2x - mx + x + 2 - m = {x^2} + 2x + xm - x - 2 - m\\ \Leftrightarrow \left( {{x^2} - {x^2}} \right) + \left( {2x - 2x} \right) - \left( {mx + mx} \right) + \left( {x + x} \right) = \left( { - 2 - 2} \right) - m + m\\ \Leftrightarrow  - 2mx + 2x =  - 4\\ \Leftrightarrow  - 2\left( {m - 1} \right)x =  - 4\\ \Leftrightarrow \left( {m - 1} \right)x = 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}$

+) TH1: $m -1 = 0$$\Leftrightarrow$ $m = 1$  

Phương trình$\,\left( 1 \right)$có dạng $0x = 2$ (phương trình vô nghiệm).

+) TH2: $m -1 \ne 0$$\Leftrightarrow$ $m \ne 1$

Phương trình$\,\left( 1 \right)$ $\Leftrightarrow$$x = \frac{2}{{m - 1}}$.

Kết hợp với điều kiện $x \ne  - 2 - m$, $x \ne  - 2 + m$ ta có:

$\left\{ \begin{array}{l}\frac{2}{{m - 1}} \ne  - 2 - m\\\frac{2}{{m - 1}} \ne  - 2 + m\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}2 \ne \left( { - 2 - m} \right)\left( {m - 1} \right)\\2 \ne \left( { - 2 + m} \right)\left( {m - 1} \right)\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}2 \ne  - 2m + 2 - {m^2} + m\\2 \ne  - 2m + 2 + {m^2} - m\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} - {m^2} - m \ne 0\\{m^2} - 3m \ne 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne  - 1\\m \ne 3\end{array} \right.$

Kết luận:

Với $m = 1$, $m = -1$,$m = 0$,$m = 3$, phương trình có tập nghiệm là: $S = \emptyset$.

Với $m \ne 0,\,\,m \ne  \pm 1,\,\,m \ne 3$, phương trình có tập nghiệm là:$S = \left\{ {\frac{2}{{m - 1}}} \right\}$.