Đề kiểm tra giữa kì II Toán 7 - Đề số 4 có lời giải chi tiết

Đề bài

I. TRẮC NGHIỆM Chọn chữ cái đặt trước câu trả lời đúng:

Câu 1: Điểm thi đua các tháng trong năm học 2013-2014 của lớp 7A được ghi trong Bảng 1:

Tần số của điểm 8 là:

     A.12 ; 1 và 4                      B. 3 

     C. 8                                   D. 10

Câu 2: Mốt của dấu hiệu điều tra trong bảng 1 là :

     A. 3                                    B. 8 

    C. 9                                     D. 10

Câu 3: Đơn thức nào sau đây đồng dạng với đơn thức $- 3x{y^2}$

     A. $- 3{x^2}y$                      B. $\left( { - 3xy} \right)y$  

    C. $- 3{\left( {xy} \right)^2}$                    D. $- 3xy$

Câu 4:  Kết quả của phép tính $- 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5}$

     A. $- 3{x^2}{y^5}$                       B. $8{x^2}{y^5}$ 

   C. $4{x^2}{y^5}$                            D. $- 4{x^2}{y^5}$

Câu 5: Giá trị của biểu thức $3{x^2}y + 3{x^2}y$ tại $x = {\rm{\;}} - 2$ và $y = {\rm{\;}} - 1$ là:

     A. 12                                  B. $- 9$ 

   C. 18                                   D. $- 24$

Câu 6: Tam giác có một góc ${60^0}$ thì với điều kiện nào thì trở thành tam giác đều :

     A. ba góc nhọn

    B. hai cạnh bằng nhau

    C. hai góc nhọn 

    D. một cạnh đáy

Lời giải chi tiết

I. TRẮC NGHIỆM

Câu 1 (NB)
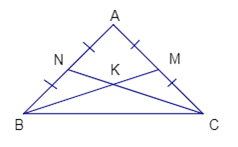
Phương pháp: Số lần xuất hiện của một giá trị trong dãy các giá trị của dấu hiệu là tần số của giá trị đó.

Quan sát bảng số liệu, đếm xem điểm 8 xuất hiện bao nhiêu lần ? số điểm 8 chính là tần số của điểm 8.
Cách giải:

Trong bảng 1, điểm 8 xuất hiện 3 lần.

Vậy tần số của điểm 8 là 3.

Chọn B

Câu 2 (NB)
Phương pháp: Mốt của dấu hiệu là giá trị có tần số lớn nhất.
Cách giải:

trong bảng 1 ta thấy điểm 8 xuất hiện với tần số lớn nhất là 3.

Vậy mốt của dấu hiệu là : điểm 8

Chọn B

Câu 3 (TH)

Phương pháp: Hai đơn thức đồng dạng là hai đơn thức có cùng hệ số, nhưng khác phần biến.

Cách giải:

Đơn thức khác hệ số và có cùng phần biến với đơn thức $- 3x{y^2}$là: $\left( { - 3xy} \right)y = {\rm{\;}} - 3x{y^2}$

Chọn B

Câu 4 (TH)
Phương pháp: Cộng các đơn thức đồng dạng, ta cộng phần hệ số với nhau và giữ nguyên phần biến.
Cách giải:

Ta có: $- 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5} = \left( { - 5 - 1 + 3} \right){x^2}{y^5} = {\rm{\;}} - 3{x^2}{y^5}$

Chọn A.

Câu 5 (TH) Phương pháp: Thu gọn đa thức rồi thay giá trị của x , y vào.
Cách giải:

Thu gọn đa thức ta được: $3{x^2}y + 3{x^2}y = 6{x^2}y$

Thay $x = {\rm{\;}} - 2;{\mkern 1mu} y = {\rm{\;}} - 1$ vào biểu thức đã được thu gọn ta có: $6.{\left( { - 2} \right)^2}\left( { - 1} \right) = {\rm{\;}} - 24$

Chọn D

Câu 6 (TH)

Phương pháp: Ta có:Tam giác cân có 1 góc bằng ${60^0}$là tam giác đều.
Cách giải:

Tam giác có một góc bằng ${60^0}$và có hai cạnh bằng nhau là tam giác đều.

Chọn B

Câu 7 (VD)

1) Phương pháp:

Lập bảng tần số theo bảng thống kê ban đầu.

Bước 1: Liệt kê các giá trị không trùng nhau.

Bước 2: Đếm số lần xuất hiện của mỗi giá trị đó. Rồi sắp xếp các số liệu tương ứng vào bảng.

Tìm mốt của dấu hiệu: là giá trị có tần số lớn nhất trong bảng tần số. Dựa trên bảng tần số và giá trị trung bình, đưa ra nhận xét.
Cách giải:

+ Bảng tần số:

+ Mốt của dấu hiệu là:

${M_0} = 80$

Chọn A

2) Phương pháp:

Điểm trung bình: Dựa vào bảng tần số, ta có thể tính số trung bình cộng của một dấu hiệu (gọi tắt là số trung bình cộng và kí hiệu là $\bar X$ ) như sau :

+ Nhân từng giá trị với tần số tương ứng.

+ Cộng tất cả các tích vừa tìm được.

+ Chia tổng đó cho số các giá trị (tức tổng các tần số).

Ta có công thức : $\bar X{\rm{\;}} = \frac{{{x_1}{n_1} + {x_2}{n_2} + {x_3}{n_3} + ... + {x_k}{n_k}}}{{\rm{N}}}$

Trong đó : ${x_1},{\mkern 1mu} {x_2},{\mkern 1mu} ....,{\mkern 1mu} {x_k}$ là k  giá trị khác nhau của dấu hiệu X.

${n_1},{\mkern 1mu} {n_2},...,{n_k}$ là k tần số tương ứng.

N là số các giá trị.
Cách giải:

Số điểm trung bình thi đua của lớp 7A là :

$\overline {X{\mkern 1mu} } {\rm{\;}} = \frac{{70.2 + 90.2 + 80.5}}{9} = 80$

Chọn D

Câu 8 (VD) Phương pháp:

1) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-góc-cạnh.

2) Chứng minh hai góc ở đáy của tam giác bằng nhau.

3) Áp dụng tính chất tam giác cân, đường trung tuyến và bất đẳng thức tam giác để chứng minh.
Cách giải:

1) Xét $\Delta BNC$ và $\Delta CMB$ có:

$\begin{array}{*{20}{l}}{BN = AN = \frac{{AB}}{2};{\mkern 1mu} }\\{CM = AM = \frac{{AC}}{2};}\\{AB = AC}\end{array}$

$\Rightarrow BN = CM$

$\angle B = \angle C$ ($\Delta ABC$ cân tại A)

BC cạnh chung.

Do đó: $\Delta BNC = \Delta CMB\left( {c.g.c} \right)$

2) Chứng minh: $\Delta KBC$ cân tại K.

Do $\Delta BNC = \Delta CMB\left( {cmt} \right)$

$\Rightarrow \angle MBC = \angle NCB$(hai góc tương ứng)

$\Rightarrow \Delta KBC$ cân tại K.

3) Chứng minh $BC < 4KM$

Ta có: $\Delta KBC$ cân tại K. (cmt)

$\Rightarrow BK = CK$

Ta có : $BK + CK = BK + BK = 2BK = 2.2KM = 4KM$ (tính chất đường trung tuyến).

Mà $\Delta KBC$ có : $KB + KC > BC$ (bất đẳng thức tam giác)

Suy ra $BC < 4.KM$ (đpcm).