Đề kiểm tra giữa kì II Toán 7 - Đề số 3 có lời giải chi tiếtĐề kiểm tra giữa kì 2 toán 7- Đề số 3 có lời giải chi tiết Đề bài Câu 1 (VD_3 điểm) Tổng số điểm 4 môn thi của các học sinh trong một phòng thi được cho trong bảng dưới đây.
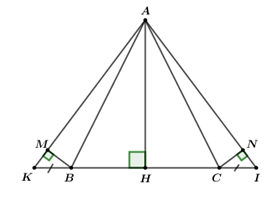
a) Dấu hiệu ở đây là gì? b) Hãy lập bảng tần số và tính trung bình cộng c) Nêu nhận xét. d) Tìm mốt của dấu hiệu Câu 2 (VD_3 điểm) Thu gọn rồi xác định phần hệ số, phần biến, bậc và tính giá trị của hai biểu thức tại \(x = 1;\,y = 2;\,z = - 2\). a) \(A = \frac{1}{2}\,{x^4}y{z^2} - \frac{3}{4}{x^4}y{z^2} + {x^4}y{z^2}\) b) \(B = 4{x^2}y.\left( { - 7} \right)xyz\) Câu 3 (VD_3,5 điểm) Cho \(\Delta ABC\) cân tại \(A\), có \(AB = AC = 13cm,\,BC = 24cm.\) Kẻ \(AH\) vuông góc với \(BC\) tại\(H\). a) Chứng minh \(\Delta AHC = \Delta AHB\) b) Tính độ dài đoạn thẳng \(AH\) c) Trên tia đối tia \(BC\) lấy điểm \(K\). Trên tia đối tia \(CB\) lấy điểm \(I\) sao cho \(BK = CI.\) Chứng minh rằng: \(\Delta ABK = \Delta ACI.\) d) Kẻ \(BM \bot AK\), \(CN \bot AI.\) Chứng minh rằng: \(\Delta MBK = \Delta NCI\). Câu 4 (VD_0,5 điểm): Một người muốn leo lên một mái nhà để sửa mái. Người đó lấy một cái thang, biết cái thang dài \(5m\) và khoảng cách từ chân thang đến nhà là \(3m\). Hỏi khoảng cách từ mặt đất lên mái nhà. Lời giải chi tiết Câu 1: Phương pháp: a) Dấu hiệu là vấn đề hay hiện tượng mà người điều tra quan tâm tìm hiểu (thường được kí hiệu bằng các chữ cái in hoa X, Y, …) b) Dựa vào số liệu đã cho lập bảng tần số, tính trung bình cộng. Công thức tính trung bình cộng: \(\overline X = \frac{{{x_1}{n_1} + {x_2}{n_2} + ... + {x_k}{n_k}}}{N}\) Trong đó: \({x_1},\,{x_2},\,....,\,{x_k}\) là \(k\) giá trị khác nhau của dấu hiệu X. \({n_1},\,{n_2},\,...,\,{n_k}\) là tần số tương ứng, \(N\) là số các giá trị. Cách giải: a) Dấu hiệu ở đây là Tổng số điểm 4 môn thi của các học sinh trong một phòng thi. Có 24 giá trị dấu hiệu. b) Bảng tần số:
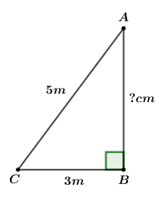
c) Nhận xét: Tổng số điểm 4 môn thi thấp nhất là 19 điểm Tổng số điểm 4 môn thi cao nhất là 39 điểm Tổng số điểm 4 môn thi chủ yếu 30 điểm chiếm 33,3% d) \({M_0} = 30\) Câu 2: Phương pháp: a) Để cộng hay trừ các đơn thức đồng dạng ta cộng hay trừ các hệ số với nhau và giữ nguyên phần biến. Xác định hệ số, phần biến, bậc của đơn thức thu được. b) Thực hiện nhân các đơn thức, ta nhân phần hệ số với nhau, nhân phần biến với nhau. Xác định hệ số, phần biến, và bậc của đơn thức tìm được. Cách giải: a) \(A = \frac{1}{2}\,{x^4}y{z^2} - \frac{3}{4}{x^4}y{z^2} + {x^4}y{z^2}\) \(\begin{array}{l} = \left( {\frac{1}{2} - \frac{3}{4} + 1} \right){x^4}y{z^2}\\ = \frac{3}{4}{x^4}y{z^2}\end{array}\) Phần hệ số: \(\frac{3}{4}\) Phần biến: \({x^4}y{z^2}\) Bậc: 7 Thay \(x = 1,\,y = 2,z = - 2\) vào biểu thức \(A\) ta được: \(A = \frac{3}{4}{.1^4}.2.{\left( { - 2} \right)^2} = 6\) b) \(B = 4{x^2}y.\left( { - 7} \right).x.y.z\) \(\begin{array}{l} = 4.\left( { - 7} \right).\left( {{x^2}.x} \right).\left( {y.y} \right).z\\ = - 28{x^3}{y^2}z\end{array}\) Phần hệ số: \( - 28.\) Phần biến: \({x^3}{y^2}z\) Bậc: 6 Thay \(x = 1,\,y = 2\,\) và \(z = - 2\) vào biểu thức \(B\); Ta được: \(B = \, - 28.\,{1^3}{.2^2}.\left( { - 2} \right) = 224\) Câu 3: Phương pháp: a) Chứng minh \(\Delta AHC = \Delta AHB\) (cạnh huyền – góc nhọn) b) Áp dụng định lý Py-ta-go cho tam giác \(\Delta ABH\) tính được cạnh \(AH\). c) \(\Delta ABK = \Delta ACI\left( {c - g - c} \right)\) d) \(\Delta MBK = \Delta NCI\) (cạnh huyền – góc nhọn) Cách giải: a) Chứng minh: \(\Delta AHC = \Delta AHB\) Xét \(\Delta AHC\) và \(\Delta AHB\) , ta có: \(\angle AHB = \angle AHC = {90^0}\) \(AB = AC\left( {gt} \right)\) \(\angle B = \angle C\) (vì \(\Delta ABC\) là tam giác cân) \( \Rightarrow \Delta AHC = \Delta AHB\,\) (cạnh huyền – góc nhọn) b) Vì \(\Delta AHC = \Delta AHB\,\)(cmt) \( \Rightarrow HB = HC\) (hai cạnh tương ứng) Nên \(H\) là trung điểm của \(BC\) \( \Rightarrow HB = HC = BC:2 = 24:2 = 12\left( {cm} \right)\) Áp dụng định lý Py-ta-go cho tam giác \(\Delta ABH\) ta có: \(A{B^2} = A{H^2} + H{B^2}\) \(\begin{array}{l}169 = A{H^2} + 144\\ \Rightarrow A{H^2} = 25\\ \Rightarrow AH = \sqrt {25} = 5\,cm\end{array}\) c) Xét \(\Delta ABK\) và \(\Delta ACI\) ta có: \(AB = AC\left( {gt} \right)\) \(\angle ABK = \angle ACI\) (góc ngoài tương ứng) \(BK = CI\left( {gt} \right)\) \( \Rightarrow \Delta ABK = \Delta ACI\left( {c - g - c} \right)\) d) Ta có: \(\Delta ABK = \Delta ACI\left( {cmt} \right)\) \( \Rightarrow \angle AKB = \angle AIC\) (hai góc tương ứng) Xét \(\Delta MBK\) và \(\Delta NCI\) ta có: \(\begin{array}{l}\angle BMK = \angle CNI = {90^0}\\BK = CI\left( {gt} \right)\\\angle BKM = \angle CIN\left( {cmt} \right)\end{array}\) \( \Rightarrow \Delta MBK = \Delta NCI\) (cạnh huyền – góc nhọn) Câu 4: Phương pháp: Áp dụng định lý Py-ta-go tính khoảng cách từ mặt đất lên mái nhà là \(4m\). Cách giải: Cái thang tạo với mặt đất và bức tường một tam giác vuông: Cạnh huyền là cái thang, hai cạnh góc vuông là khoảng cách từ chân thang đến nhà và khoảng cách từ mặt đất lên mái nhà. Ta có hình vẽ: + \(AC\) là độ dài cái thang + \(CB\) khoảng cách từ chân thang đến tường + \(AB\) là khoảng cách từ mặt đất lên mái nhà Áp dụng định lý Pytago cho \(\Delta ABC\) ta có: \(\begin{array}{l}A{B^2} = A{C^2} - B{C^2} = {5^2} - {3^2} = {4^2}\\ \Rightarrow AB = 4\,m\end{array}\) Vậy khoảng cách từ mặt đất lên mái nhà là \(4\,m\).
|