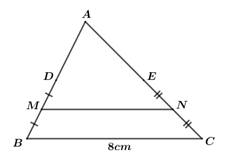
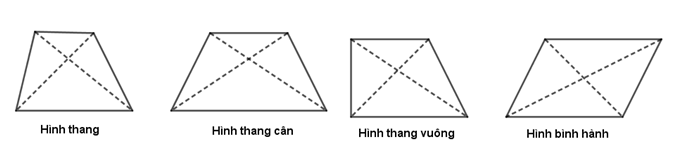
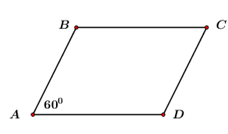
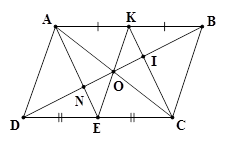
Đề kiểm tra giữa kì 1 Toán 8 - Đề số 4 có lời giải chi tiết

Đề bài

PHẦN I: TRẮC NGHIỆM (2 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng trong mỗi câu sau vào bài làm.

Câu 1: Kết quả phép tính \(x\left( {x - y} \right) + y\left( {x + y} \right)\) tại \(x =  - 3\) và \(y = 4\) là:

A. \(1\)                                            B. \(7\)                                    

C. \( - 25\)                                       D. \(25\)

Câu 2: Khai triển biểu thức \({\left( {x - 2y} \right)^3}\) ta được kết quả là:

A. \({x^3} - 8{y^3}\)                                           

B. \({x^3} - 2{y^3}\)                          

C. \({x^3} - 6{x^2}y + 6x{y^2} - 2{y^3}\)       

D. \({x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}\)

Câu 3: Giá trị biểu thức \({2009^2} - 2018.2009 + {1009^2}\) có bao nhiêu chữ số \(0\)?

A. \(6\)                                     B. \(2\)                                    

C. \(4\)                                     D. \(0\)

Câu 4: Đa thức \(4{x^2} - 12x + 9\) phân tích thành nhân tử là:

A. \({\left( {2x - 3} \right)^2}\)                                 B. \(2x + 3\)                            

C. \(4x - 9\)                                  D. \({\left( {2x + 3} \right)^2}\)

Câu 5: Hình nào sau đây là tứ giác có hai đườg chéo bằng nhau?

A. Hình thang                          B. Hình thang cân                  

C. Hình thang vuông              D. Hình bình hành

Câu 6: Cho tam giác \(ABC\) có cạnh \(BC = 8cm\) và \(D,\,\,E,\,\,M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC,\,\,BD\) và \(CE\) (như hình vẽ). Khi đó, \(MN = ?\)

Tìm \(x\), biết: \(3x\left( {x - 5} \right) - {x^2} + 25 = 0\)

Câu 4 (3,0 điểm) Cho hình bình bình hành \(ABCD\,\,\left( {AB > AD} \right)\). Gọi \(E\) và \(K\) lần lượt là trung điểm của \(CD\) và \(AB.\)\(BD\) cắt \(AE,\,\,AC\) và \(CK\) lần lượt tại \(N,\,\,O\) và \(I\). Chứng minh rằng

a) Tứ giác \(AECK\) là hình bình hành.

b) Ba điểm \(E,\,\,O,\,\,K\) thẳng hàng.

c) \(DN = NI = IB\)

d) \(AE = 3KI\)

Câu 5 (1,0 điểm) Cho \(x,\,\,y\) là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:

\(P = {x^2} + 5{y^2} + 4xy + 6x + 16y + 32\)

Lời giải chi tiết

A. PHẦN TRẮC NGHIỆM

1. D	2. D	3. A	4. A
5. B	6. C	7. A	8. C

 

Câu 1:

Phương pháp:

Cách 1: Thay trực tiếp giá trị của \(x,\,\,y\) vào biểu thức

Cách 2: Rút gọn biểu thức sau đó thay giá trị của \(x,\,\,y\)

Cách giải:

Thay \(x =  - 3\) và \(y = 4\) vào biểu thức \(x\left( {x - y} \right) + y\left( {x + y} \right)\) ta được:

\(\left( { - 3} \right)\left( { - 3 - 4} \right) + 4.\left( { - 3 + 4} \right) = 21 + 4 = 25\)

Chọn D.

Câu 2:

Phương pháp:

Áp dụng hằng đẳng thức “Lập phương của một hiệu”.

Cách giải:

Ta có: \({\left( {x - 2y} \right)^3}\)\( = {x^3} - 3{x^2}.2y + 3x{\left( {2y} \right)^2} + {\left( {2y} \right)^3}\)\( = {x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}\)

Chọn D.

Câu 3:

Phương pháp:

Áp dụng hằng đẳng thức: \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}.\)

Cách giải:

\(\begin{array}{l}\,\,\,\,{2009^2} - 2018.2009 + 1009\\ = {2009^2} - 2.2009.1009 + 1009\\ = {\left( {2009 - 1009} \right)^2}\\ = {1000^2}\\ = 1000\,000\end{array}\)

Vậy giá trị của biểu thức \({2009^2} - 2018.2009 + {1009^2}\) có \(6\) chữ số \(0\).

Chọn A.

Câu 4:

Phương pháp:

Áp dụng phương pháp dùng hằng đẳng thức: \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}.\)

Cách giải:

\(4{x^2} - 12x + 9\)\( = {\left( {2x} \right)^2} - 2.2x.3 + {3^2} = {\left( {2x - 3} \right)^2}\)

Chọn A.

Câu 5:

Phương pháp:

Áp dụng định nghĩa, tính chất của mỗi hình.

Cách giải:

Trong các hình ở các đáp án, chỉ có hình thanh cân có hai đường chéo bằng nhau.

Chọn B.

Câu 6:

Phương pháp:

Sử dụng tính chất của tam giác và hình thang để làm bài toán.

Cách giải:

Xét \(\Delta ABC\) ta có:  \(D,\,\,E\) lần lượt là trung điểm của \(AB,\,\,AC\)

\( \Rightarrow DE\)  là đường trung bình của \(\Delta ABC\) (định nghĩa đường trung bình)

\( \Rightarrow \left\{ \begin{array}{l}DE\,{\rm{//}}\,BC\\\,\,DE = \frac{1}{2}BC\end{array} \right.\) (tính chất đường trung bình của tam giác)

\( \Rightarrow DE = \frac{1}{2}BC = \frac{1}{2}.8 = 4\,\,cm.\)

Vì \(DE\,{\rm{//}}\,BC\) nên tứ giác \(DECB\) là hình thang.

Xét hình thang \(DECB\) ta có: \(M,\,\,N\) lần lượt là trung điểm của \(BD,\,\,EC\)

\( \Rightarrow MN\) là đường trung bình của hình thang \(DECB\) (định nghĩa đường trung bình)

\( \Rightarrow \left\{ \begin{array}{l}MN//DE\,\,{\rm{//}}\,BC\\\,\,MN = \frac{1}{2}\left( {DE + BC} \right)\end{array} \right.\) (tính chất đường trung bình của tam giác)

\( \Rightarrow MN = \frac{1}{2}\left( {DE + BC} \right) = \frac{1}{2}\left( {8 + 4} \right) = 6\,\,cm.\)

Vậy \(MN = 6cm\).

Chọn D.

Câu 7:

Phương pháp:

Áp dụng các tính chất của hình bình hành.

Cách giải:

Vì \(ABCD\) là hình bình hành nên ta có: \(\angle A = \angle C,\,\,\angle B = \angle D\) và \(AB\,{\rm{//}}\,CD,AD\,{\rm{//}}\,BC\) (tính chất hình bình hành).

Mà \(\angle A = {60^0} \Rightarrow \angle C = {60^0}\)

\( \Rightarrow \) Đáp án C đúng.

Vì  \(AD\,{\rm{//}}\,BC\) mà \(\angle A\) và \(\angle B\) ở vị trí trong cùng phía nên ta có: \(\angle A + \angle B = {180^0}\)\( \Rightarrow \angle B = {120^0}\)

\( \Rightarrow \angle B = \angle D = {120^0}\) \( \Rightarrow \) Đáp án A sai.

\( \Rightarrow \angle B = 2\angle C\)\( \Rightarrow \) Đáp án B đúng.

\( \Rightarrow \angle A = \frac{{\angle B}}{2}\)\( \Rightarrow \) Đáp án D đúng.

Chọn A.

Câu 8:

Phương pháp:

Sử dụng định lý Pitago để tính độ dài các đường chéo của hình chữ nhật.

Trong hình chữ nhật, độ dài hai đường chéo bằng nhau nên khoảng cách từ giao điểm của hai đường chéo đến mỗi đỉnh = nửa đường chéo.

Cách giải:

Độ dài đường chéo của hình chữ nhật \(ABCD\) là: \(\sqrt {{5^2} + {{12}^2}}  = 13\left( {cm} \right)\)

Vậy khoảng cách từ giao điểm của hai đường chéo đến mỗi đỉnh là: \(\frac{{13}}{2}cm = 6,5\,\,cm.\)

Chọn C.

PHẦN II: TỰ LUẬN

Câu 1:

Phương pháp:

a) Áp dụng quy tắc nhân đơn thức với đa thức.

b) Khai triển hằng đẳng thức, áp dụng quy tắc nhân đơn thức với đa thức.

c) Áp dụng quy tắc chia đa thức cho đơn thức.

Cách giải:  

\(\begin{array}{l}a)\,\,\,2x\left( {3x + 2} \right) - 3x\left( {2x + 3} \right)\\ = 2x.3x + 2x.2 - 3x.2x - 3x.3\\ = 6{x^2} + 4x - 6{x^2} - 9x\\ =  - 5x\end{array}\) \(\begin{array}{l}c)\,\,\,\,\left( {3{x^3} - 4{x^2} + 6x} \right):3x\\ = 3{x^3}:3x - 4{x^2}:3x + 6x:3x\\ = {x^2} - \frac{4}{3}x + 2\end{array}\)

\(\begin{array}{l}b)\,\,\,\,{\left( {x + 2} \right)^3} + {\left( {x - 3} \right)^2} - {x^2}\left( {x + 5} \right)\\ = \left( {{x^3} + 6{x^2} + 12x + 8} \right) + \left( {{x^2} - 6x + 9} \right) - \left( {{x^3} + 5{x^2}} \right)\\ = {x^3} + 6{x^2} + 12x + 8 + {x^2} - 6x + 9 - {x^3} - 5{x^2}\\ = \left( {{x^3} - {x^3}} \right) + \left( {6{x^2} + {x^2} - 5{x^2}} \right) + \left( {12x - 6x} \right) + 8 + 9\\ = 2{x^2} + 6x + 17\end{array}\)

Câu 2:

Phương pháp:

Áp dụng phương pháp đặt nhân tử chung và dùng hằng đẳng thức.

Cách giải:

\(\begin{array}{l}\,\,\,\,2{x^3} - 12{x^2} + 18x\\ = 2x\left( {{x^2} - 6x + 9} \right)\\ = 2x{\left( {x - 3} \right)^2}\end{array}\)

Câu 3:

Phương pháp:

Áp dụng phương pháp phân tích đa thức thành nhân tử.

Cách giải:

\(\begin{array}{l}\,\,\,\,\,\,\,\,3x\left( {x - 5} \right) - {x^2} + 25 = 0\\ \Leftrightarrow 3x\left( {x - 5} \right) - \left( {{x^2} - 25} \right) = 0\\ \Leftrightarrow 3x\left( {x - 5} \right) - \left( {x + 5} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {3x - x - 5} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {2x - 5} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - 5 = 0\\x - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{5}{2}\\x = 5\end{array} \right.\end{array}\)

Vậy \(x \in \left\{ {\frac{5}{2};\,\,5} \right\}\).

Câu 4:

Phương pháp:

a) Áp dụng dấu hiệu nhận biết hình bình hành.

b) Áp dụng tính chất của hình bình hành.

c) Áp dụng tính chất đường trung bình trong tam giác.

d) Áp dụng tính chất đường trung bình trong tam giác, cộng đoạn thẳng.

Cách giải:

a) Tứ giác \(AECK\) là hình bình hành.

Vì \(ABCD\) là hình bình hành nên: \(\left\{ \begin{array}{l}AB\,{\rm{//}}\,CD\\AB = CD\end{array} \right.\) (tính chất của hình bình hành)

Mà \(E,\,\,K\) lần lượt là trung điểm của \(CD\) và \(AB\) nên \(AK = EC = \frac{1}{2}AB\) và \(AK\,{\rm{//}}\,EC\).

\( \Rightarrow \) Tứ giác \(AECK\) là hình bình hành (dhnb).

b) Ba điểm \(E,\,\,O,\,\,K\) thẳng hàng.

Trong hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo nên \(O\) là trung điểm của \(AC\) và \(BD\) (tính chất của hình bình hành).

Mà \(AECK\) là hình bình hành  (cmt) nên \(O\) là trung điểm của \(EK\).

\( \Rightarrow \) Ba điểm \(E,\,\,O,\,\,K\) thẳng hàng.

c) \(DN = NI = IB\)

Vì \(AECK\) là hình bình hành nên \(AE\,{\rm{//}}\,CK\) (tính chất của hình bình hành)

Xét \(\Delta DIC\) ta có: \(\left. \begin{array}{l}ED = EC\,\,\,\left( {gt} \right)\\EN\,{\rm{//}}\,CI\,\,\,\left( {AE//CK} \right)\end{array} \right\} \Rightarrow DN = NI\) (định lý đảo)

Tương tự, xét \(\Delta ABN\) ta có: \(\left. \begin{array}{l}KA = KB\left( { = \frac{1}{2}AB} \right)\\KI\,{\rm{//}}\,AN\,\,\,\left( {KC//AE} \right)\end{array} \right\} \Rightarrow BI = NI\) (định lý đảo)

\( \Rightarrow DN = BI = NI\) (đpcm).

d) \(AE = 3KI\)

Ta có: \(KI\) là đường trung bình của \(\Delta ABN\,\,\left( {cmt} \right)\)\( \Rightarrow KI = \frac{1}{2}AN\)

\(EN\) là đường trung bình của \(\Delta DCI\,\,\left( {cmt} \right)\)\( \Rightarrow EN = \frac{1}{2}IC\)

\( \Rightarrow AE = AN + NE = 2KI + \frac{1}{2}IC\)\( = \frac{3}{2}KI + \frac{1}{2}KI + \frac{1}{2}IC = \frac{3}{2}KI + \frac{1}{2}KC\)

\( \Rightarrow AE = \frac{3}{2}KI + \frac{1}{2}AE\) \( \Rightarrow \frac{1}{2}AE = \frac{3}{2}KI \Rightarrow AE = 3KI\)

Vậy \(AE = 3KI\).

Câu 5:

Phương pháp:

Áp dụng phương pháp nhóm, dùng hằng đẳng thức để đưa đa thức đã cho về dạng \(P = {A^2} + {B^2} + a\). Trong đó, \(A,\,\,B\) là các đa thức và \(a\) là hằng số.

Cách giải:

\(\begin{array}{l}\,\,\,\,\,\,P = {x^2} + 5{y^2} + 4xy + 6x + 16y + 32\\ \Leftrightarrow P = {x^2} + \left( {4xy + 6x} \right) + 5{y^2} + 16y + 32\\ \Leftrightarrow P = {x^2} + 2x\left( {2y + 3} \right) + {\left( {2y + 3} \right)^2} - {\left( {2y + 3} \right)^2} + 5{y^2} + 16y + 32\\ \Leftrightarrow P = {\left[ {x + \left( {2y + 3} \right)} \right]^2} - 4{y^2} - 12y - 9 + 5{y^2} + 16y + 32\\ \Leftrightarrow P = {\left( {x + 2y + 3} \right)^2} + {y^2} + 4y + 23\\ \Leftrightarrow P = {\left( {x + 2y + 3} \right)^2} + {\left( {y + 2} \right)^2} + 19\end{array}\)

Vì \({\left( {x + 2y + 3} \right)^2} \ge 0\) với mọi \(x,\,\,y \in \mathbb{R}\).

     \({\left( {y + 2} \right)^2} \ge 0\) với mọi \(y \in \mathbb{R}\)

\( \Rightarrow P = {\left( {x + 2y + 3} \right)^2} + {\left( {y + 2} \right)^2} + 19 \ge 19\) với mọi \(x,\,\,y \in \mathbb{R}\).

Dấu “\( = \)” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}x + 2y + 3 = 0\\y + 2 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x + 2y =  - 3\\y =  - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 2\end{array} \right.\)  

Vậy \(P\) đạt giá trị nhỏ nhất bằng \(19\) khi \(x = 1\) và \(y =  - 2\).