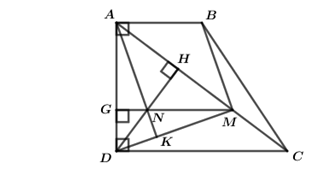
Đề kiểm tra giữa kì 1 Toán 8 - Đề số 1 có lời giải chi tiết

Đề bài

Câu 1 (2 điểm) Thực hiện các phép tính sau:

a) \(3x\left( {5{x^2} + 2x - 1} \right)\)                                                b) \(\left( {x + 1} \right)\left( {x - 2} \right)\)

c) \( - 8{x^3}{y^2}:2xy\)                                             d) \(\left( {5{x^4} - 3{x^3} + {x^2}} \right):3{x^2}\)

Câu 2 (2 điểm)

a) Rút gọn biểu thức: \(A = {\left( {x + 1} \right)^2} + {\left( {x - 1} \right)^2} - \left( {x - 1} \right)\left( {x + 1} \right).\)

b) Tìm \(x,\) biết: \({x^2} - x = 0.\)

Câu 3 (2,0 điểm) Phân tích các đa thức sau thành nhân tử:

a) \({x^2} - {y^2} - 2x - 2y\)                                       b) \({a^2} - 9 - 8ab + 16{b^2}\)

Câu 4 (3,5 điểm) Cho hình thang vuông \(ABCD\) \(\left( {\angle A = \angle D = {{90}^0}} \right)\) và \(CD = 2AB\). Kẻ \(DH\) vuông góc với \(AC\)\(\left( {H \in AC} \right)\). Gọi \(M\) là trung điểm của \(HC\), \(N\) là trung điểm của \(DH\). Chứng minh rằng:

a) \(MN \bot AD\)

b) \(ABMN\) là hình bình hành.

c) \(\angle BMD = {90^0}\)

Câu 5 (0,5 điểm) Tìm các số \(a,b,c \in \mathbb{Q}\) biết \({a^2} + {b^2} + {c^2} = ab + bc + ac\) và \(a + b + c = 2019\).

Lời giải chi tiết

Câu 1

Phương pháp:

a) Áp dụng quy tắc nhân đơn thức với đa thức.

b) Áp dụng quy tắc nhân đa thức với đa thức.

c) Áp dụng quy tắc chia đơn thức với đơn thức.

d) Áp dụng quy tắc chia đa thức với đơn thức.

Cách giải:

a) \(3x\left( {5{x^2} + 2x - 1} \right)\)\( = 3x.5{x^2} + 3x.2x - 3x.1\)\( = 15{x^3} + 6{x^2} - 3x\)

b) \(\left( {x + 1} \right)\left( {x - 2} \right)\) \( = ({x +1}) .x - ({x +1}) .2 \)\( = x.x - x.2 + 1.x - 1.2\) \( = {x^2} - 2x + x - 2\)\( = {x^2} - x - 2\)

c) \( - 8{x^3}{y^2}:2xy =  - 4{x^2}y\)

d) \(\left( {5{x^4} - 3{x^3} + {x^2}} \right):3{x^2}\)\( = 5{x^4}:3{x^2} - 3{x^3}:3{x^2} + {x^2}:3{x^2}\)\( = \frac{5}{3}{x^2} - x + \frac{1}{3}\)

Câu 2

Phương pháp:

a) Áp dụng hằng đẳng thức để rút gọn biểu thức.

b) Áp dụng phương pháp đặt thừa số chung để tìm \(x\).

Cách giải:

a) Rút gọn biểu thức:

\(\begin{array}{l}A = {\left( {x + 1} \right)^2} + {\left( {x - 1} \right)^2} - \left( {x - 1} \right)\left( {x + 1} \right)\\\,\,\,\,\, = \left( {{x^2} + 2x + 1} \right) + \left( {{x^2} - 2x + 1} \right) - \left( {{x^2} - 1} \right)\\\,\,\,\,\, = {x^2} + 2x + 1 + {x^2} - 2x + 1 - {x^2} + 1\\\,\,\,\,\, = {x^2} + 3\end{array}\)

Vậy \(A = {x^2} + 3\).

b) Tìm \(x\), biết:

\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} - x = 0 \Leftrightarrow x\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array}\)

Vậy \(x \in \left\{ {0;\,\,1} \right\}\).

Câu 3

Phương pháp:

a. Áp dụng phương pháp nhóm hạng tử và đặt thừa số chung để phân tích đa thức thành nhân tử.

b. Áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử.

Cách giải:

Phân tích các đa thức sau thành nhân tử:

\(\begin{array}{l}a)\,\,\,\,{x^2} - {y^2} - 2x - 2y\\ = \left( {{x^2} - {y^2}} \right) - \left( {2x + 2y} \right)\\ = \left( {x - y} \right)\left( {x + y} \right) - 2\left( {x + y} \right)\\\, = \left( {x - y - 2} \right)\left( {x + y} \right)\end{array}\)

Vậy \({x^2} - {y^2} - 2x - 2y = \left( {x - y - 2} \right)\left( {x + y} \right)\)

\(\begin{array}{l}b)\,\,\,{a^2} - 9 - 8ab + 16{b^2}\\ = \left( {{a^2} - 8ab + 16{b^2}} \right) - 9\\\, = {\left( {a - 4b} \right)^2} - {3^2}\\\, = \left( {a - 4b - 3} \right)\left( {a - 4b + 3} \right)\end{array}\)

Vậy \({a^2} - 9 - 8ab + 16{b^2} = \left( {a - 4b - 3} \right)\left( {a - 4b + 3} \right)\).

Câu 4

Phương pháp:

a) Áp dụng tính chất đường trung bình của tam giác.

b) Áp dụng dấu hiệu nhận biết hình bình hành.

c) Áp dụng định nghĩa hình bình hành, từ vuông góc đến song song, tính chất ba đường cao của tam giác.

Cách giải:

a) Chứng minh \(MN \bot AD.\)

Vì \(ABCD\) là hình thang vuông có \(\angle A = \angle D = {90^0}\).

\( \Rightarrow AD \bot DC = \left\{ D \right\}\) (1)

Xét tam giác \(HDC\) ta có:

\(M,\,\,N\) lần lượt là trung điểm của \(HC,\,\,HD\,\,\,\left( {gt} \right)\)

\( \Rightarrow NM\) là đường trung bình của tam giác \(HDC\). (định nghĩa đường trung bình)

\( \Rightarrow NM\,{\rm{//}}\,DC\) (2)

Từ (1) và (2) suy ra \(MN \bot AD\) tại \(G\) (từ vuông góc đến song song).

b) Chứng minh \(ABMN\) là hình bình hành.

Theo giả thiết, ta có: \(CD = 2AB \Rightarrow AB = \frac{1}{2}CD\)

Mà \(MN\) là đường trung bình của tam giác \(HDC\,\,\,\left( {cmt} \right)\)  \( \Rightarrow MN = \frac{1}{2}DC\).

\( \Rightarrow AB = MN\left( { = \frac{1}{2}CD} \right).\).

Lại có:  \(\left. \begin{array}{l}AB\,{\rm{//}}\,CD\,\,\,\,\left( {gt} \right)\\MN\,{\rm{//}}\,CD\,\,\,\left( {cmt} \right)\end{array} \right\} \Rightarrow AB\,{\rm{//}}\,MN\).

Xét tứ giác \(ABMN\) ta có:

\(AB = MN\)

\(AB\,{\rm{//}}\,MN\)

\( \Rightarrow ABMN\) là hình bình hành (dhnb).

c) Chứng minh \(\angle BMD = {90^0}.\)

Kẻ \(AN\) cắt \(DM\) tại \(K\).

Ta có:

\(\left. \begin{array}{l}MG \bot AD\,\,\,\,\left( {cmt} \right)\\DH \bot AM\,\,\,\left( {gt} \right)\\MG \cap DH = \left\{ N \right\}\end{array} \right\} \Rightarrow N\) là trực tâm của tam giác \(ADM\)

\( \Rightarrow AK \bot DM\) tại \(K\)

Ta có: \(ABMN\) là hình bình hành (cmt)

\( \Rightarrow BM\,{\rm{//}}\,AK\) \( \Rightarrow BM\, \bot \,DM\) (từ song song đến vuông góc)

\( \Rightarrow \angle BDM = {90^0}\,\,\,\left( {dpcm} \right)\)

Câu 5

Phương pháp:

Đưa về dạng biểu thức đa cho về dạng \({A^2} + {B^2} + {C^2} = 0 \Rightarrow A = B = C = 0\).

Cách giải:

Theo giả thiết, ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,{a^2} + {b^2} + {c^2} = ab + bc + ac\\ \Leftrightarrow 2\left( {{a^2} + {b^2} + {c^2}} \right) = 2\left( {ab + bc + ac} \right)\\ \Leftrightarrow 2{a^2} + 2{b^2} + 2{c^2} = 2ab + 2bc + 2ac\\ \Leftrightarrow 2{a^2} + 2{b^2} + 2{c^2} - 2ab - 2bc - 2ac = 0\\ \Leftrightarrow {a^2} - 2ab + {b^2} + {a^2} - 2ac + {c^2} + {b^2} - 2bc + {c^2} = 0\\ \Leftrightarrow {\left( {a - b} \right)^2} + {\left( {a - c} \right)^2} + {\left( {b - c} \right)^2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}a - b = 0\\a - c = 0\\b - c = 0\end{array} \right. \Rightarrow a = b = c\end{array}\)

Ta lại có: \(a + b + c = 2019 \Rightarrow a = b = c = \frac{{2019}}{3}\).

Vậy \(a = b = c = \frac{{2019}}{3}\).