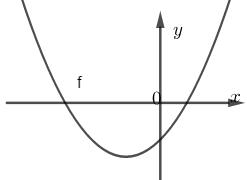
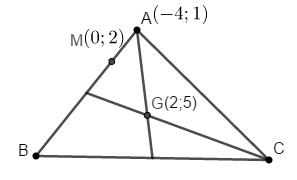
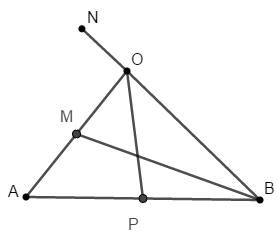
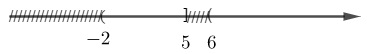Đề kiểm tra giữa kì 1 Toán 10 - đề số 4 có lời giải chi tiết

Đề bài

Câu 1. Cho mệnh đề chứa biến P(x) với \(x \in {\rm{X}}\). Mệnh đề phủ định của mệnh đề “\(\forall x \in X,P(x)\)” là

A. “\(\exists x \in X,\overline {P(x)} \)”

B. “\(\exists x \in X,P(x)\)”

C. “\(\forall x \in X,\overline {P(x)} \)”

D. “\(\forall x \notin X,P(x)\)”

Câu 2. Gọi M là trung điểm cạnh AB của tam giác ABC. Khi đó

A. \(\overrightarrow {MA}  = \overrightarrow {MB} \)        B. \(\overrightarrow {MC}  = \overrightarrow {MA} \)   

C. \(\overrightarrow {AM}  = \overrightarrow {MB} \)       D. \(\overrightarrow {MC}  = \overrightarrow {MB} \)

Câu 3.  Cho tập hợp \(A = \left\{ {x \in \mathbb{N}\left| {\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} + 3x - 4} \right) = 0} \right.} \right\}\). Số phần tử của A là

A. 1         B. 2         C. 3           D. 4

Câu 4. Cho các điểm \(A\left( {1;0} \right);B\left( {2; - 6} \right);C\left( {3;25} \right);D\left( {4;60 + \sqrt 2 } \right)\) Có bao nhiêu điểm thuộc đồ thị \(\left( C \right)\) của hàm số \(y = {x^3} - x + \sqrt {x - 2} \)?

A. 2          B. 3              C. 4            D. 5

Câu 5. Trong hệ trục tọa độ Oxy, tọa độ của vec tơ \(\overrightarrow i  - \overrightarrow j \) là

A. \(\left( {1; - 1} \right)\)        B. \(\left( { - 1;1} \right)\)         C. \(\left( {0; - 1} \right)\)      D. \(\left( {1;1} \right)\)

Câu 6. Hình nào dưới đây biểu diễn \(\left( { - 2;5} \right] \cup \left( {6; + \infty } \right)\)?

A.

B.

C.

D.

Câu 7. Cho 2 mệnh đề \(P\): “Hình thang ABCD có hai cạnh bên song song”. \(Q\):“\(ABCD\) là hình bình hành”. Mệnh đề \(P \Rightarrow Q\) là

A.  Nếu \(ABCD\) là hình bình hành thì nó là hình thang có hai cạnh bên song song.

B. Nếu hình thang ABCD có hai cạnh bên song song thì nó là hình bình hành.

C. \(ABCD\) là hình bình hành khi và chỉ khi hình thang ABCD có hai cạnh bên song song.

D. Hình thang có hai cạnh bên bằng nhau là hình bình hành.

Câu 8. Cho hàm số \(y = ax + b\left( {a \ne 0} \right)\). Mệnh đề nào sau đây đúng?

A. Nếu \(a > 0\) thì hàm số làm hàm chẵn

B. Nếu \(a > 0\) thì hàm số nghịch biến trên \(\mathbb{R}\)

C. Hàm số trên là hàm lẻ nếu đường thẳng đi qua gốc tọa độ.

D. Nếu \(a < 0\) thì hàm số đồng biến trên \(\mathbb{R}\)

Câu 9. Đồ thị dưới đây là đồ thị của hàm số

 

A. \(y = \dfrac{1}{2}{x^2} + 2x - 1\)

B. \(y = \dfrac{{\sqrt 2 }}{3}{x^2} + 2x - 3\)

C. \(y = \dfrac{{2 - \sqrt 3 }}{2}{x^2} + x - 4\)

D. \(y = 100x + 1\)

Câu 10. Tập xác định của hàm số \(y = \dfrac{{\sqrt {2x + 5} }}{{x - 1}} - 2\) là

A. \(\left( {1; + \infty } \right)\)          B. \(\left[ { - \dfrac{5}{2}; + \infty } \right)\)    C. \(\left[ { - \dfrac{5}{2};1} \right) \cup \left( {1; + \infty } \right)\)   D. \(\left[ { - \dfrac{5}{2};1} \right]\)

Câu 11. Khẳng định nào sai trong các khẳng định sau:

A. Hàm số \(y = \sqrt {1 - x}  + \sqrt {1 + x} \) là hàm số chẵn.

B. hàm số \(y = \left| {x + 2} \right| - \left| {x - 2} \right|\) là hàm số lẻ.

C. Hàm số \(y = {\left( {2x - 1} \right)^2}\) là hàm số lẻ.

D. Hàm số \(y =  - 2{x^2} + 3\) là hàm số chẵn.

Câu 12. Trong các hàm số sau, hàm số nào là hàm số bậc nhất?

A. \(y = \dfrac{{ - x + 2}}{{3x + 1}}\)             B. \(y =  - \dfrac{1}{2}x + \dfrac{{3\sqrt 2 }}{{\sqrt 5  - 7}}\)

C. \(y = {x^2} + 2\)               D.\(y = \left| {x + 3} \right|\)

Câu 13. Cho hàm số \(y = \dfrac{1}{2}{x^2} - 2\left( {m + 1} \right)x + 2\). Tìm m để hàm số có trục đối xứng đi qua điểm \(A\left( {0;1} \right)\).

A. \(m =  - \dfrac{1}{2}\)         B. \(m = \dfrac{1}{2}\)        C. \(m = 0\)         D. \(m = 1\)

Câu 14. Giao điểm của đường thẳng \(y = 2x + 6\) và parabol \(\left( P \right):y =  - {x^2} - x + 2\) là

A. \(M\left( { - 1;4} \right)\)           B. \(M\left( {0;2} \right)\)

C. \(M\left( { - 1;2} \right)\)           D. Không có giao điểm

Câu 15. Tam giác ABC có \(A\left( { - 4;1} \right)\), trọng tâm \(G\left( {2;5} \right)\), điểm \(M\left( {0;2} \right)\) là điểm trên đoạn AB sao cho \(BM = 3AM\).  Tọa độ của B, C lần lượt là

A. \(B\left( { - 12;1} \right),C\left( {22;15} \right)\)

B. \(B\left( { - 12; - 1} \right),C\left( {22;15} \right)\)

C. \(B\left( {12;1} \right),C\left( { - 22;15} \right)\)

D. \(B\left( {12; - 1} \right),C\left( { - 2;15} \right)\)

Câu 16. Giải phương trình \(\left| {x - 2} \right| - 4 = 0\)

A. \(x = 6\) hoặc \(x = 2\)

B. \(x = 2\) hoặc \(x =  - 2\)

C. \(x =  - 6\) hoặc \(x =  - 2\)

D. \(x =  - 2\) hoặc \(x = 6\)

Câu 17. Cho tam giác OAB. Gọi M, P lần lượt là trung điểm của OA, AB. N là điểm trên OB sao cho \(\overrightarrow {ON}  =  - \dfrac{1}{3}\overrightarrow {OB} \). Tìm m, n sao cho \(\overrightarrow {OP}  = m\overrightarrow {OM}  + n\overrightarrow {ON} \)

A. \(m = 1,n =  - 1\)         B. \(m = 1,n =  - \dfrac{3}{2}\)

C. \(m = 1,n = \dfrac{3}{2}\)        D. \(m =  - 1,n =  - \dfrac{3}{2}\)

Câu 18. Cho \(a <  - 1\) thỏa mãn \(\overrightarrow {AB}  = a\overrightarrow {CA} \). Khi đó

A. \(\overrightarrow {AB} ,\overrightarrow {AC} \)cùng hướng

B. \(\overrightarrow {AB} ,\overrightarrow {BC} \) cùng hướng

C. \(\overrightarrow {AB} ,\overrightarrow {CA} \) cùng hướng

D. \(\overrightarrow {AC} ,\overrightarrow {CB} \) ngược hướng

Câu 19. Cho tam giác đều ABC cạnh a có G là trọng tâm. Độ dài của vec tơ \(\overrightarrow {AC}  - \overrightarrow {BG} \) là

A. \(\dfrac{a}{6}\)           B. \(\dfrac{{a\sqrt 3 }}{3}\)         C. \(\dfrac{a}{3}\)            D. \(\dfrac{{2a\sqrt 3 }}{3}\)

Câu 20. Cho tam giác ABC. E là điểm trên đoạn AB sao cho \(\overrightarrow {AE}  = \dfrac{1}{4}\overrightarrow {AB} \). N là trung điểm của AC. Tập hợp điểm M thỏa mãn\(\overrightarrow {MA}  - \dfrac{1}{2}\overrightarrow {AB}  + \overrightarrow {MC}  = \overrightarrow 0 \). Khi đó:

A.  AENM là hình bình hành

B. BENM là hình bình hành

B. CENM là hình bình hành

C. ABNM là hình bình hành

Câu 21. Một công xưởng sản xuất một lô áo gồm 300 chiếc áo với giá vốn là 45000000 (đồng) và giá bán mỗi chiếc áo là 300000 đồng. Gọi X là số tiền của công xưởng thu được khi bán t chiếc áo. Để lời được 9000000 đồng thì cần phải bán ít nhất bao nhiêu chiếc áo?

A. 180                B. 30          C. 90          D. 120

Câu 22. Giải phương trình \(\sqrt {x + 1}  = x - 1\)

A. \(x = 0\)      B. \(x = 3\)        C. \(x = 0\) hoặc \(x = 3\)      D. \(x = 1\)

Câu 23. Tìm m để đường thẳng \(\left( d \right):y = \dfrac{{ - 2m - 1}}{3}\) cắt đồ thị của hàm số \(\left( P \right):y = {x^2} - 3\left| x \right| + 1\) tại đúng 2 điểm phân biệt.

A. \(m = 0\)                             B. \(m < 0\)     

C.  \(m = 0\) hoặc \(m >  - 2\)      D. \(m = 0\) hoặc \(m <  - 2\)

Câu 24. Cho tam giác ABC có G là trọng tâm, I là điểm thỏa mãn \(\overrightarrow {AI}  =  - \dfrac{1}{2}\overrightarrow {AC} \). Điểm M thỏa mãn \(\overrightarrow {AM}  = x\overrightarrow {AB} \)( x là số thực). Tìm x để M, G, I thẳng hàng.

A. \(x = \dfrac{1}{3}\)             B. \(x = 3\)       C. \(x = \dfrac{1}{5}\)            D. \(x = \dfrac{5}{3}\)

Câu 25.  Tịnh tiến đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 5\) theo vectơ nào thì được đồ thị \(\left( {P'} \right)\) của hàm số \(y = {x^2} - 2x + 5\)

A. \(\overrightarrow v  = \left( { - 1;2} \right)\)     B. \(\overrightarrow v  = \left( {1; - 1} \right)\)    C. \(\overrightarrow v  = \left( {1;1} \right)\)       D. \(\overrightarrow v  = \left( {1;0} \right)\)

Lời giải chi tiết

Câu	1	2	3	4	5	6	7	8	9
Đáp án	A	C	B	A	C	A	B	C	C
Câu	10	11	12	13	14	15	16	17	18
Đáp án	C	C	B	A	D	B	D	B	A
Câu	19	20	21	22	23	24	25
Đáp án	D	A	A	D	B	C	B

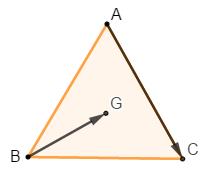
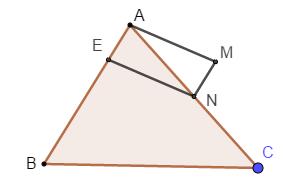
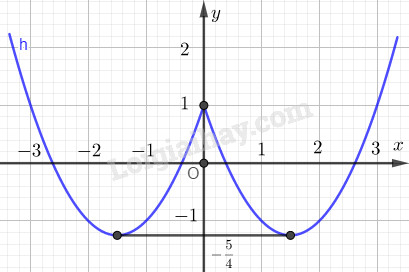
Câu 1. Mệnh đề phủ định của mệnh đề “\(\forall x \in X,P(x)\)” là “\(\exists x \in X,\overline {P(x)} \)”.

Câu 2. Do M là trung điểm của AB nên \(\overrightarrow {AM}  = \overrightarrow {MB} \)

Câu 3.

\(\begin{array}{l}\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} + 3x - 4} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right)\left( {x - 1} \right)\left( {x + 4} \right) = 0\\\left[ \begin{array}{l}x =  - 1 \notin \mathbb{N}\\x = 2 \in \mathbb{N}\\x = 1 \in \mathbb{N}\\x =  - 4 \notin \mathbb{N}\end{array} \right.\end{array}\)

Vậy \(A = \left\{ {1;2} \right\} \to \)Có 2 phần tử.

Câu 4.

TXĐ: \(D = \left[ {2; + \infty } \right)\) \( \Rightarrow A \notin \left( C \right)\).

Thay lần lượt tọa độ các điểm B, C, D vào hàm số ta được:

\({2^3} - 2 + \sqrt {2 - 2}  = 6 \ne  - 6 \Rightarrow B \notin (C)\)

\({3^3} - 3 + \sqrt {3 - 1} 2 = 25 \Rightarrow C \in (C)\)

\({4^3} - 4 + \sqrt {4 - 2}  = 60 + \sqrt 2  \Rightarrow D \in \left( C \right)\)

Vậy có 2 điểm thuộc đồ thị của (C).

Câu 8.

TXĐ: \(D = \mathbb{R}\).

Ta có \(x \in \mathbb{R} \Rightarrow  - x \in \mathbb{R}\).

Đường thằng đi qua gốc tọa độ nên \(0 = a.0 + b \Rightarrow b = 0\).

Với \(x \in D\) tùy ý, \(f\left( { - x} \right) =  - ax =  - f\left( x \right)\).

Vậy hàm số \(y =  - ax + b\) là hàm lẻ nếu hàm số đi qua gốc tọa độ.

Câu 9. Hàm số có bề lõm hướng lên trên nên \(a < 0\). Các đáp án A, B, D đều có \(a > 0\) nên loại. Đáp án C có \(a < 0\).

Câu 10. ĐKXĐ:

\(\left\{ \begin{array}{l}2x + 5 \ge 0\\x - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge  - \dfrac{5}{2}\\x \ne 1\end{array} \right. \Rightarrow D = \left[ { - \dfrac{5}{2};1} \right) \cup \left( {1; + \infty } \right)\)

Câu 11.

Xét hàm số \(y = {\left( {2x - 1} \right)^2}\) có:

\(f\left( { - x} \right) = {\left( { - 2x - 1} \right)^2} \ne  - {\left( {2x - 1} \right)^2} \Rightarrow f\left( { - x} \right) \ne  - f\left( x \right)\)

Vậy hàm số \(y = {\left( {2x - 1} \right)^2}\) không phải là hàm số lẻ.

Câu 12.

Hàm số bậc nhất là hàm số được cho dưới dạng \(y = ax + b\left( {a \ne 0} \right)\) nên hàm số \(y =  - \dfrac{1}{2}x + \dfrac{{3\sqrt 2 }}{{\sqrt 5  - 7}}\) là hàm số bậc nhất.

Câu 13.

Trục đối xứng của đồ thị hàm số \(y = \dfrac{1}{2}{x^2} - 2\left( {m + 1} \right)x + 2\) là :

\(y = 2\left( {m + 1} \right)\). Đường thẳng này đi qua điểm \(A\) khi và chỉ khi:

\(2\left( {m + 1} \right) = 1 \Leftrightarrow m =  - \dfrac{1}{2}\)

Câu 14.

Hoành độ giao điểm của của đường thẳng \(y = 2x + 6\) và parabol \(\left( P \right):y =  - {x^2} - x + 2\) là nghiệm của phương trình:

\( - {x^2} - x + 2 = 2x + 6 \Leftrightarrow {x^2} + 3x + 4 = 0\)(1)

\({\Delta _{\left( 1 \right)}} = {3^2} - 4.4 =  - 7 < 0\) nên (1) vô nghiệm.

Vậy đường thẳng \(y = 2x + 6\) và parabol \(\left( P \right):y =  - {x^2} - x + 2\) không có giao điểm.

Câu 15.

 

Ta có: \(\overrightarrow {MA}  = \left( { - 4; - 1} \right)\)

\(\overrightarrow {MB}  = 3\overrightarrow {MA}  = \left( { - 12; - 3} \right)\)\( \Rightarrow B\left( { - 12; - 1} \right)\)

Ta có G là trọng tâm tam giác ABC nên

\(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B} = 22\\{y_C} = 3{y_G} - {y_A} - {y_B} = 15\end{array} \right.\)

Vậy \(B\left( { - 12; - 1} \right),C\left( {22;15} \right)\).

Câu 16.

\(\begin{array}{l}\left| {x - 2} \right| - 4 = 0 \Leftrightarrow \left| {x - 2} \right| = 4\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 4\\x - 2 =  - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 6\\x =  - 2\end{array} \right.\end{array}\)

Câu 17.

 

Ta có:

\(\begin{array}{l}\overrightarrow {OP}  = \dfrac{1}{2}\left( {\overrightarrow {OA}  + \overrightarrow {OB} } \right) = \dfrac{1}{2}\overrightarrow {OA}  + \dfrac{1}{2}\overrightarrow {OB} \\ = \overrightarrow {OM}  + \dfrac{1}{2}.\left( { - 3} \right)\overrightarrow {ON}  = \overrightarrow {OM}  - \dfrac{3}{2}\overrightarrow {ON} \end{array}\)

Vậy \(m = 1,n =  - \dfrac{3}{2}\)

Câu 18.

Ta có \(a <  - 1\) nên \(\overrightarrow {AB} ,\overrightarrow {CA} \) ngược hướng và \(AB > AC\). Hay \(\overrightarrow {AB} ,\overrightarrow {AC} \)cùng hướng và C nằm giữa A và B.

Câu 19.

 

Ta có G là trọng tâm tam giác ABC nên \(GB \bot AC\) và \(GB = \dfrac{{a\sqrt 3 }}{3}\).

Vẽ hình bình hành \(BGCD\). Khi đó \(\overrightarrow {BG}  = \overrightarrow {DC} \)\( \Rightarrow CD = \dfrac{{a\sqrt 3 }}{3}\)

\(\overrightarrow {AC}  - \overrightarrow {BG}  = \overrightarrow {AC}  + \overrightarrow {CD}  = \overrightarrow {AD} \)\( \Rightarrow \left| {\overrightarrow {AC}  - \overrightarrow {BG} } \right| = AD\)

Vì \(GB \bot AC\) nên \(AC \bot CD\). Suy ra \(AD = \sqrt {{a^2} + \dfrac{{{a^2}}}{3}}  = \dfrac{{2a\sqrt 3 }}{3}\).

Vậy \(\left| {\overrightarrow {AC}  - \overrightarrow {BG} } \right| = \dfrac{{2a\sqrt 3 }}{3}\).

Câu 20.

 

N là trung điểm của AC nên \(\overrightarrow {MA}  + \overrightarrow {MC}  = 2\overrightarrow {MN} \).

Ta có:

\(\begin{array}{l}\overrightarrow {MA}  - \dfrac{1}{2}\overrightarrow {AB}  + \overrightarrow {MC}  = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MC}  = \dfrac{1}{2}\overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {MN}  = \dfrac{1}{4}\overrightarrow {AB}  = \overrightarrow {AE} \end{array}\)

Khi đó M là điểm thỏa mãn AENM là hình bình hành.

Câu 21.

Hàm số của X  theo t là:

\(y = 300000t\left( {0 \le t \le 300} \right)\)

Hàm số biểu diễn số tiền lời (hoặc lỗ) khi bán được t chiếc áo là

\(y = 300000t - 45000000\)

Để lời được 9000000 thì \(300000t - 45000000 = 9000000 \Leftrightarrow t = 180\)

Vậy cần bán được 180 chiếc áo.

Câu 22.

\(\begin{array}{l}\sqrt {x + 1}  = x - 1 \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\x + 1 = {\left( {x - 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 3x = 0\end{array} \right. \Leftrightarrow x = 3\end{array}\)

Câu 23.

Ta có hàm số (P): \(y = \left\{ \begin{array}{l}{x^2} - 3x + 1{\rm{  khi }}x \ge 0\\{x^2} + 3x + 1{\rm{  khi }}x < 0\end{array} \right.\)

Vẽ đồ thị của hàm số \(\left( P \right):y = {x^2} - 3\left| x \right| + 1\).

• Vẽ Parabol \(({P_1}):y = {x^2} - 3x + 1\). Bỏ đi phần đồ thị bên trái trục tung.
• Vẽ Parabol \(({P_2}):y = {x^2} + 3x + 1\) bằng cách lấy đối xứng \(\left( {{P_1}} \right)\) qua trục \(Oy\).

Ta được đồ thị của \(\left( P \right):y = {x^2} - 3\left| x \right| + 1\) như sau:

 

Từ đồ thị ta thấy \(\left( d \right):y = \dfrac{{ - 2m - 1}}{3}\) cắt \(\left( P \right)\) tại đúng 2 điểm phân biệt khi và chỉ khi \(\left[ \begin{array}{l}\dfrac{{ - 2m - 1}}{3} = 0\\\dfrac{{ - 2m - 1}}{3} > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m =  - \dfrac{1}{2}\\m <  - 2\end{array} \right.\)

Câu 24.

M, G, I thẳng hàng \( \Leftrightarrow \) tồn tại số k để \(\overrightarrow {IG}  = k\overrightarrow {IM} \)

\(\begin{array}{l}\overrightarrow {IG}  = \dfrac{1}{3}\left( {\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC} } \right) = \dfrac{1}{3}\overrightarrow {IA}  + \dfrac{1}{3}\left( {\overrightarrow {IA}  + \overrightarrow {AB} } \right) + \dfrac{1}{3}\left( {\overrightarrow {IA}  + \overrightarrow {AC} } \right)\\ = \overrightarrow {IA}  + \dfrac{1}{3}\overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {AC}  = \dfrac{5}{6}\overrightarrow {AC}  + \dfrac{1}{3}\overrightarrow {AB} \end{array}\)

\(\overrightarrow {IM}  = \overrightarrow {IA}  + \overrightarrow {AM}  = \dfrac{1}{2}\overrightarrow {AC}  + x\overrightarrow {AB} \)

Do đó \(\dfrac{5}{6}\overrightarrow {AC}  + \dfrac{1}{3}\overrightarrow {AB}  = k\left( {\dfrac{1}{2}\overrightarrow {AC}  + x\overrightarrow {AB} } \right) = \dfrac{k}{2}\overrightarrow {AC}  + kx\overrightarrow {AB} \).

Đồng nhất hệ số ta được \(\left\{ \begin{array}{l}k = \dfrac{5}{3}\\x = \dfrac{1}{5}\end{array} \right.\)

Câu 25.

Gọi \(\overrightarrow v \left( {a;b} \right)\) là vectơ tịnh tiến. \(M\left( {x;y} \right) \in (P)\) tùy ý, \(M'\left( {x';y'} \right)\) là ảnh của \(M\) qua \({T_{\overrightarrow v }}\), khi đó:

\(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

\(\overrightarrow v \left( {a;b} \right)\) là vectơ tịnh tiến biến \(\left( P \right)\) thành \(\left( {P'} \right)\) khi và chỉ khi \(M' \in (P')\).

 \( \Leftrightarrow {\left( {x + a} \right)^2} - 2\left( {x + a} \right) + 5 = y + b\)

\( \Leftrightarrow y = {x^2} + \left( {2a - 2} \right)x + {a^2} - 2a + 5 - b\)

Mà ta có \(M \in \left( P \right)\) nên \(y = {x^2} + 5\). Đồng nhất hệ số ta được:

\(\left\{ \begin{array}{l}2a - 2 = 0\\{a^2} - 2a + 5 - b = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 1\end{array} \right.\)

Vậy \(\overrightarrow v  = \left( {1; - 1} \right)\)

HocTot.Nam.Name.Vn