Đề kiểm tra giữa kì 1 Toán 10 - đề số 1 có lời giải chi tiết

Đề bài

Câu 1. (2,5 điểm)

a) Cho tập \(A,B\) lần lượt là tập xác định của hàm số \(f\left( x \right) = \sqrt {x - 6} \) và \(g\left( x \right) = \dfrac{3}{{2x + 1}}\). Xác định các tập \(A \cap B,A \cup B,A\backslash B,{C_\mathbb{R}}A\).

b) Cho tập hợp \(C = \left[ { - 3;8} \right]\) và \(D = \left[ {m - 6;m + 3} \right)\). Với giá trị nào của \(m\) thì \(C \cap D\) là một đoạn thẳng có độ dài bằng 4.

Câu 2.(1,5 điểm)

1) Xét tính chẵn lẻ của hàm số sau: \(y = f\left( x \right) = \dfrac{{{x^2} + 1}}{{\left| {2x + 1} \right| + \left| {2x - 1} \right|}}\).

2) Cho đường thẳng \(\left( d \right)\): \(y = \left| {3x + 2} \right| - 2\). Khi tịnh tiến \(\left( d \right)\) lên trên 1 đơn vị, rồi sang phải 2 đơn vị, ta được đồ thị của hàm số nào?

Câu 3. (2,5 điểm) Cho hàm số \(y = 3{x^2} - 2x + 3\) có đồ thị là một parabol \((P)\).

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số trên.

b) Tìm tất cả giá trị của \(m\) để đồ thị hàm số \(y = x - m\) cắt (P) tại 2 điểm phân biệt có hoành độ dương.

Câu 4. (3,5 điểm) Cho tam giác \(ABC\) vuông cân tại \(A\)có \(BC = 6\sqrt 2 cm\). Gọi \(M,N\) là các điểm thỏa mãn \(\overrightarrow {AM}  = \dfrac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN}  = \dfrac{1}{4}\overrightarrow {AC} \).

a) Tính \(\left| {\overrightarrow {AM}  + \overrightarrow {AN} } \right|\).

b) Chứng minh rằng \(4\overrightarrow {MN}  - \overrightarrow {AC}  + 2\overrightarrow {AB}  = \overrightarrow 0 \).

c) Gọi D là trung điểm của BC. Tìm tập hợp điểm E thỏa mãn \(\left| {\overrightarrow {EM}  + \overrightarrow {EN}  - \overrightarrow {ED} } \right| = \dfrac{1}{2}AC\).

Lời giải chi tiết

Câu 1.

a) Ta có \(f\left( x \right) = \sqrt {x - 6}  \Rightarrow \)ĐKXĐ: \(x - 6 \ge 0 \Leftrightarrow x \ge 6\)

\( \Rightarrow A = \left[ {6; + \infty } \right)\)

\(g\left( x \right) = \dfrac{3}{{2x + 1}} \Rightarrow \)ĐKXĐ: \(2x + 1 \ne 0 \Leftrightarrow x \ne  - \dfrac{1}{2}\)

\( \Rightarrow B = \mathbb{R}\backslash \left\{ { - \dfrac{1}{2}} \right\}\)

Ta có:\(A \subset B\) nên \(A \cap B = \left[ {6; + \infty } \right)\);\(A \cup B = \mathbb{R}\backslash \left\{ { - \dfrac{1}{2}} \right\}\);\(A\backslash B = \emptyset \);

\({C_\mathbb{R}}A = \left( { - \infty ;6} \right)\).

b) \(C \cap D\) là một đoạn thẳng có độ dài bằng 4 khi và chỉ khi

\(8 - \left( {m - 6} \right) = 4 \Leftrightarrow m =  - 10\)

Câu 2.

a) TXĐ: \(D = \mathbb{R}\)

Khi đó, \(\forall x \in D \Rightarrow  - x \in D\).

\(\begin{array}{l}f\left( { - x} \right) = \dfrac{{{{\left( { - x} \right)}^2} + 1}}{{\left| { - 2x + 1} \right| + \left| { - 2x - 1} \right|}}\\ = \dfrac{{{x^2} + 1}}{{\left| { - \left( {2x - 1} \right)} \right| + \left| { - \left( {2x + 1} \right)} \right|}}\\ = \dfrac{{{x^2} + 1}}{{\left| {2x - 1} \right| + \left| {2x + 1} \right|}} = f\left( x \right)\end{array}\)

Vậy hàm số \(y = f\left( x \right)\) là hàm chẵn.

b) Kí hiệu \(f\left( x \right) = \left| {3x + 2} \right| - 2\).

Khi tịnh tiến \(\left( d \right)\) lên trên 1 đơn vị ta được đồ thị \(\left( {{d_1}} \right)\) của hàm số: \(y = f\left( x \right) + 1 = \left| {3x + 2} \right| - 1\).

Kí hiệu \(g\left( x \right) = \left| {3x + 2} \right| - 1\). Khi tịnh tiến \(\left( {{d_1}} \right)\) sang phải 2 đơn vị ta được đồ thị \(\left( {{d_2}} \right)\) của hàm số: \(y = g\left( {x - 2} \right) = \left| {3\left( {x - 2} \right) + 2} \right| - 1 = \left| {3x - 4} \right| - 1\).

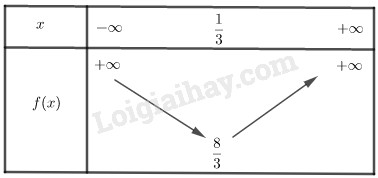
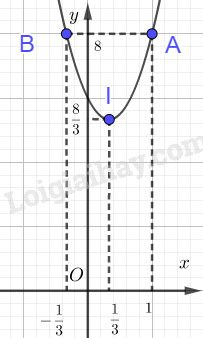
Câu 3.

a) TXĐ: \(D = \mathbb{R}\)

Ta có \( - \dfrac{b}{{2a}} = \dfrac{1}{3};\dfrac{{ - \Delta }}{{4a}} = \dfrac{8}{3}\). Đồ thị hàm số có đỉnh \(I\left( {\dfrac{1}{3};\dfrac{8}{3}} \right)\) và trục đối xứng là \(x = \dfrac{1}{3}\) và hướng bề lõm lên trên. Từ đó ta có hàm số nghịch biến trên \(\left( { - \infty ;\dfrac{1}{3}} \right)\), đồng biến trên \(\left( {\dfrac{1}{3}; + \infty } \right)\).

Bảng biến thiên:

Từ bảng biến thiên ta thấy hàm số có giá trị nhỏ nhất là \(\dfrac{8}{3}\) khi \(x = \dfrac{1}{3}\).

Ta có: (P) cắt trục tung tại điểm \(\left( {0;3} \right)\), không cắt trục hoành, \((P)\) đi qua điểm \(A\left( {1;4} \right),B\left( { - \dfrac{1}{3};4} \right)\).

Đồ thị:

b) Phương trình hoành độ giao điểm của đường thẳng \(d\) và đồ thị \((P)\) là:

\(\begin{array}{l}3{x^2} - 2x + 3 = x - m\\ \Leftrightarrow 3{x^2} - 3x + 3 - m = 0(1)\end{array}\)

Đồ thị hàm số \(y = x - m\) cắt (P) tại 2 điểm phân biệt có hoành độ dương

\( \Leftrightarrow \)Phương trình (1) có 2 nghiệm phân biệt dương \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta  > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 4.3.\left( {3 - m} \right) > 0\\3 - m > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{3}{4}\\m < 3\end{array} \right.\end{array}\)

Vậy \(\dfrac{3}{4} < m < 3\)

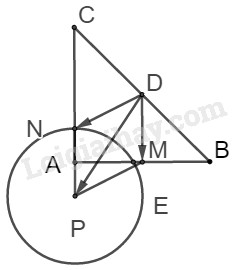
Câu 4.

a) Ta có: \(\Delta ABC\) vuông cân tại A có \(BC = 6\sqrt 2 \) nên \(AB = AC = 6(cm)\).

\(\begin{array}{l}{\left( {\overrightarrow {AM}  + \overrightarrow {AN} } \right)^2} = A{M^2} + 2\overrightarrow {AM} .\overrightarrow {AN}  + A{N^2}\\ = A{M^2} + A{N^2} = \dfrac{1}{4}A{B^2} + \dfrac{1}{{16}}A{C^2}\\ = \dfrac{5}{{16}}A{B^2} \Rightarrow \left| {\overrightarrow {AM}  + \overrightarrow {AN} } \right| = \dfrac{{\sqrt 5 }}{4}AB = \dfrac{{3\sqrt 5 }}{2}\left( {cm} \right)\end{array}\)

b) Ta có

\(\begin{array}{l}4\overrightarrow {MN}  - \overrightarrow {AC}  + 2\overrightarrow {AB} \\ = 4\left( {\overrightarrow {AN}  - \overrightarrow {AM} } \right) - \overrightarrow {AC}  + 2\overrightarrow {AB} \\ = \overrightarrow {AC}  - 2\overrightarrow {AB}  - \overrightarrow {AC}  + 2\overrightarrow {AB}  = \overrightarrow 0 \end{array}\)

c) Kẻ hình bình hành \(MDNP\). Ta có

 \(\begin{array}{l}\overrightarrow {EM}  + \overrightarrow {EN}  - \overrightarrow {ED}  = \overrightarrow {EM}  + \overrightarrow {DN} \\ = \overrightarrow {ED}  + \overrightarrow {DM}  + \overrightarrow {DN}  = \overrightarrow {ED}  + \overrightarrow {DP}  = \overrightarrow {EP} \end{array}\)

\( \Rightarrow \)tập hợp điểm \(E\) cần tìm là đường tròn tâm \(P\) bán kính \(3cm\).

HocTot.Nam.Name.Vn