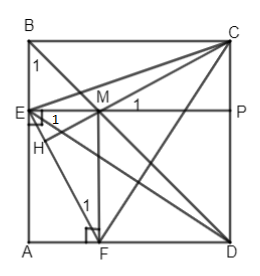
Đề kiểm tra 15 phút - Đề số 5 - Bài 12 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 12 - Chương 1 - Hình học 8 Đề bài Cho hình vuông ABCD. Từ điểm M tùy ý trên đường chéo BD, kẻ ME, MF lần lượt vuông góc với AB và AD. Chứng minh MC = EF và \(MC \bot {\rm{EF}}\). Phương pháp giải - Xem chi tiết Sử dụng: Tính chất hình vuông, hình chữ nhật Tứ giác có hai cặp cạnh đối song song là hình bình hành Hình bình hành có một góc vuông là hình chữ nhật Lời giải chi tiết
Vẽ \(MP \bot CD.\) Ta có \(MP//AD\) (vì \(AD \bot CD)\), lại có \(ME// AD \Rightarrow MP\) và ME phải trùng nhau (tiên đề Ơ clit) hay ba điểm E, M, P thẳng hàng. Tứ giác BCPE có BC//EP (cùng vuông góc với CD) và BE//CP (do ABCD là hình vuông) nên BCPE là hình bình hành. Lại có góc B vuông (do ABCD là hình vuông) nên tứ giác BCPE là hình chữ nhật \( \Rightarrow BE = CP.\) Mặt khác \(\Delta BEM\) vuông cân (vì \(\widehat {{B_1}} = {45^ \circ }\)) \( \Rightarrow BE = ME\) và M thuộc BD là tia phân giác của góc ADC nên MF = MP. Do đó hai tam giác vuông \(\Delta EMF = \Delta CPM(c.g.c)\) \( \Rightarrow EF = MC\) và \(\widehat {{F_1}} = \widehat {{M_1}}.\) Gọi H là giao điểm của CM và EF ta có \(\widehat {{M_1}} = \widehat {{M_2}}\) (đối đỉnh) \( \Rightarrow \widehat {{M_2}} = \widehat {{F_1}}\) mà \(\widehat {{F_1}} + \widehat {{E_1}} = {90^ \circ }(\Delta EMF\) vuông ) \( \Rightarrow \widehat {{M_2}} + \widehat {{E_1}} = {90^ \circ } \Rightarrow \widehat {MHE} = {90^ \circ }\) hay \(MC \bot {\rm{EF}}{\rm{.}}\) Nhận xét: *Để chứng minh MC = EF, bạn có thể chứng minh MC = MA vì M thuộc BD mà BD là đường trung trực của đoạn AC (tính chất hai đường chéo của hình vuông). *Ta có thể chứng minh được ba đường sau đây đồng quy CM, BF, DE khi chúng là đường cao của \(\Delta CEF.\) HocTot.Nam.Name.Vn
|