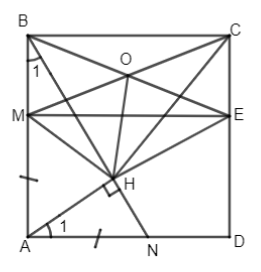
Đề kiểm tra 15 phút - Đề số 2 - Bài 12 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 12 - Chương 1 - Hình học 8 Đề bài Cho hình vuông ABCD. Trên cạnh AB lấy M bất kì, trên AD lấy N sao cho AM = AN, kẻ AH vuông góc với BN, AH cắt CD tại E \(\left( {H \in BN} \right)\). Tính \(\widehat {MHC}\). Phương pháp giải - Xem chi tiết Sử dụng: Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành Hình bình hành có một góc vuông là hình chữ nhật Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
Lời giải chi tiết
Hai tam giác vuông ABN và ADE có \(AB = AD;\widehat {{A_1}} = \widehat {{B_1}}\) (cùng phụ với\(\widehat {BAH}\) ) \( \Rightarrow \Delta ABN = \Delta DAE\left( {g.c.g} \right)\) \( \Rightarrow AN = DE\left( { = AM} \right)\) \( \Rightarrow BM = CE.\) Do ABCD là hình vuông nên AB//CD và góc B vuông Tứ giác BMEC có BM=CE, BM//CE nên là hình bình hành. Lại có góc B vuông nên BMEC là hình chữ nhật. Gọi O là giao điểm hai đường chéo BE và CM, ta có OB = OE = OC = OM. Mặt khác ta có BHE vuông có HO là trung tuyến \( \Rightarrow OH = OB = OC\) (tính chất trung tuyến của tam giác vuông) \( \Rightarrow OH = OC = OM =\dfrac{MC}2\Rightarrow \Delta MHC\) vuông hay \(\widehat {MHC} = {90^ \circ }\) . HocTot.Nam.Name.Vn
|