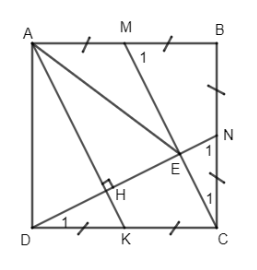
Đề kiểm tra 15 phút - Đề số 4 - Bài 12 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 12 - Chương 1 - Hình học 8 Đề bài Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB và BC. Gọi E là giao điểm của CM và DN. a) Chứng minh \(CM \bot DN\) tại E. b) Gọi K là trung điểm của DC và AH là đường cao của \(\Delta ADE\) . Chứng minh rằng ba điểm A, H, K thẳng hàng. Phương pháp giải - Xem chi tiết Sử dụng: Tính chất hai tam giác bằng nhau Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành Lời giải chi tiết
a) Xét hai tam giác vuông CBM và DCN có NB=NC, BC=DC (vì ABCD là hình vuông) Suy ra \(\Delta CBM = \Delta DCN\left( {c.g.c} \right)\) \( \Rightarrow \widehat {{C_1}} = \widehat {{D_1}}\) và \(\widehat {{M_1}} = \widehat {{N_1}}\) Mà \(\widehat {{M_1}} + \widehat {{C_1}} = {90^ \circ }\) (vì \(\widehat {MBC} = {90^ \circ })\) \( \Rightarrow \widehat {{N_1}} + \widehat {{C_1}} = {90^ \circ }\) Trong đó \(\Delta CEN\) ta có \(\widehat {CEN} = {180^ \circ } - \left( {\widehat {{N_1}} + \widehat {{C_1}}} \right) = {90^ \circ }\) Chứng tỏ \(CM \bot DN.\) b) Vì K là trung điểm CD, M là trung điểm AB mà \(AB//CD\) và AB = CD (do ABCD là hình vuông) \( \Rightarrow CK//AM\) và CK = AM. Do đó AMCK là hình bình hành \( \Rightarrow AK//CM\) mà \(AH// CM\left( { \bot DN} \right).\) Vậy AK và AH phải trùng nhau (tiên đề Ơ clit) hay ba điểm A, H, K thẳng hàng. HocTot.Nam.Name.Vn
|