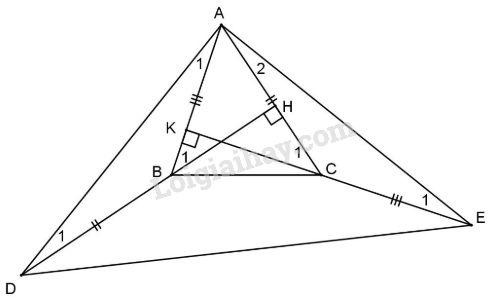
Đề kiểm tra 15 phút - Đề số 2 - Bài 9 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC có ba góc nhọn, hai đường cao BH và CK. Trên tia đối của tia BH lấy D sao cho \(BD = AC\), trên tia đối của tia CK lấy điểm E sao cho \(CE = AB\). Chứng minh \(\Delta A{\rm{D}}E\) vuông cân.

Lời giải chi tiết

Ta có \({\widehat B_1} = {\widehat C_1}\) (cùng phụ với \(\widehat {BAC}\))

\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\) (kề bù với  \({\widehat B_1} = {\widehat C_1}\))

Xét \(\Delta AB{\rm{D}}\) và \(\Delta EC{\rm{A}}\) có:

+) \(AB = CE\) (gt);

+) \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\) (cmt);

+) \(BD = AC\) (gt);

Do đó \(\Delta AB{\rm{D}} = \Delta EC{\rm{A}}\) (c.g.c)

\( \Rightarrow {\widehat A_1} = {\widehat E_1}\) và \({\widehat A_3} = {\widehat D_1}\) (góc tương ứng).

\(\Delta ABH\) vuông tại H (gt)

\({\widehat B_1} + \widehat {BAC} = {90^0}\) mà \({\widehat B_1} = {\widehat A_1} + {\widehat D_1}\) (góc ngoài của \(\Delta AB{\rm{D}}\)) và \({\widehat D_1} = {\widehat A_2}\) (cmt).

Do đó  \({\widehat A_1} + \widehat {BAC} + {\widehat A_2} = {90^0},\) lại có \(AD = AE\) (cmt).

Vậy \(\Delta A{\rm{D}}E\) vuông cân.

HocTot.Nam.Name.Vn