Nội dung từ Loigiaihay.Com
Câu hỏi:
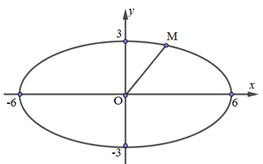
Cho Elip (E):x236+y29=1, M là điểm bất kì thuộc (E). Khi đó, giá trị lớn nhất của OM là:
- A 3
- B 6
- C 5
- D 9
Phương pháp giải:
- Quan sát đồ thị, dễ dàng nhận thấy rằng OM lớn nhất khi M trùng với điểm (6;0) hoặc (−6;0).
- Sử dụng phương pháp thế và đánh giá để chứng minh nhận xét trên.
Lời giải chi tiết:
M∈(E)⇒M(x0;y0):x0236+y029=1⇔x02=36−4y02
Ta có: OM2=x02+y02=36−4y02+y02=36−3y02≤36
⇒OM≤6⇒OMmax khi và chỉ khi {y_0} = 0 \Leftrightarrow {x_0} = \pm 6
Chọn: B













