25 bài tập phương trình đường elip mức độ nhận biếtLàm bàiCâu hỏi 1 : Cho elip (E) có phương trình chính tắc là \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Gọi \(2c\) là tiêu cự của (E). Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án: C Phương pháp giải: Áp dụng lý thuyết phương trình chính tắc của elip. Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\) với \(a > b > 0\) và \({a^2} = {b^2} + {c^2}\) với \(2c\) là tiêu cự của (E). Lời giải chi tiết: Theo lý thuyết phương trình chính tắc của elip có \({a^2} = {b^2} + {c^2}\) Đáp án: C Câu hỏi 2 : Elip (E) có độ dài trục bé bằng tiêu cự. Tâm sai của (E) là:
Đáp án: A Phương pháp giải: Tính tỉ số \(e = {c \over a}\) trong đó \(2c\) là tiêu cự của elip \(2a\) là độ dài trục lớn của elip \(2b\) là độ dài trục bé của elip Và ta có \({a^2} = {b^2} + {c^2}\)Lời giải chi tiết: Elip có độ dài trục bé bằng tiêu cự nên ta có \(b = c\). Mặt khác ta có \({a^2} = {b^2} + {c^2}\), suy ra \({a^2} = 2{c^2}\) hay \(a = \sqrt 2 c\). Tâm sai của elip là: \(e = {c \over a} = {c \over {\sqrt 2 c}} = {1 \over {\sqrt 2 }}\). Đáp án: A Câu hỏi 3 : Cho elip \((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) và cho các mệnh đề: I. \((E)\) có các tiêu điểm \({F_1}(0; - 4)\) và \({F_2}(0;4)\) II. \((E)\) có tỉ số \({c \over a} = {4 \over 5}\) III. \((E)\) có đỉnh \({A_1}( - 5;0)\) IV. \((E)\) có độ dài trục nhỏ bằng 3. Tìm mệnh đề sai trong các mệnh đề sau:
Đáp án: D Phương pháp giải: Từ phương trình của elip và lý thuyết elip tìm các hệ số \(a,b,c\) rồi kết luận. Lời giải chi tiết: Từ phương trình elip \((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) ta có \(\left\{ \matrix{ a = 5 \hfill \cr b = 3 \hfill \cr c = \sqrt {{a^2} - {b^2}} = 4 \hfill \cr} \right.\) Suy ra ta có: I. \((E)\) có các tiêu điểm \({F_1}( - 4;0)\) và \({F_2}(4;0)\) II. \((E)\) có tỉ số \({c \over a} = {4 \over 5}\) III. \((E)\) có đỉnh \({A_1}( - 5;0)\) IV. \((E)\) có độ dài trục nhỏ bằng \(2b = 6\). Đáp án: D Câu hỏi 4 : Elip có độ dài trục lớn là 12, độ dài trục nhỏ là 8 có phương trình chính tắc là:
Đáp án: A Phương pháp giải: Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\) Elip có độ dài trục lớn bằng \(2a\) Elip có độ dài trục bé bằng \(2b\)Lời giải chi tiết: Độ dài trục lớn là 12, suy ra \(2a = 12\) hay \(a = 6\) Độ dài trục nhỏ là 8, suy ra \(2b = 8\) hay \(b = 4\) Vậy elip cần tìm là \({{{x^2}} \over {36}} + {{{y^2}} \over {16}} = 1\) Đáp án: A Câu hỏi 5 : Phương trình chính tắc của elip có hai đỉnh là \(A(5;0)\) và \(B(0;3)\) là:
Đáp án: C Phương pháp giải: Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\) Chú ý Elip có 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\) Lời giải chi tiết: Elip có hai đỉnh là \(A(5;0)\) và \(B(0;3)\) suy ra \(a = 5\) và \(b = 3\). Do đó, phương trình chính tắc của elip là: \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) Đáp án: C Câu hỏi 6 : Cho elip chính tắc (E) có tiêu điểm \({F_1}(4;0)\) và một đỉnh là \(A(5;0)\). Phương trình chính tắc của elip (E) là:
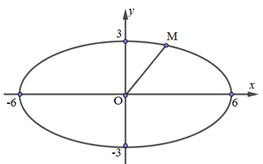
Đáp án: C Phương pháp giải: Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\). Elip có 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\) Elip có tiêu cự bằng \(2c\) và ta cũng có \({a^2} = {b^2} + {c^2}\)Lời giải chi tiết: Elip có tiêu điểm \({F_1}(4;0)\) suy ra \(c = 4\), elip có một đỉnh là \(A(5;0)\) suy ra \(a = 5\). Mặt khác ta có \({b^2} = {a^2} - {c^2} = 25 - 16 = 9\). Vậy elip có phương trình là \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\). Đáp án: C Câu hỏi 7 : Cho Elip \((E):\,\,{{{x^2}} \over {36}} + {{{y^2}} \over 9} = 1\), \(M\) là điểm bất kì thuộc (E). Khi đó, giá trị lớn nhất của \(OM\) là:
Đáp án: B Phương pháp giải: - Quan sát đồ thị, dễ dàng nhận thấy rằng OM lớn nhất khi M trùng với điểm \((6;\,0)\) hoặc \(( - 6;0)\). - Sử dụng phương pháp thế và đánh giá để chứng minh nhận xét trên. Lời giải chi tiết:
\(M \in (E) \Rightarrow M({x_0};{y_0}):\,\,\,\,{{{x_0}^2} \over {36}} + {{{y_0}^2} \over 9} = 1 \Leftrightarrow {x_0}^2 = 36 - 4{y_0}^2\) Ta có: \(O{M^2} = {x_0}^2 + {y_0}^2 = 36 - 4{y_0}^2 + {y_0}^2 = 36 - 3{y_0}^2 \le 36\) \( \Rightarrow OM \le 6\,\,\,\,\,\,\, \Rightarrow O{M_{\max }} = 6\) khi và chỉ khi \({y_0} = 0 \Leftrightarrow {x_0} = \pm 6\) Chọn: B Câu hỏi 8 : Cho Elip \((E):\,\,9{x^2} + 16{y^2} = 144\), \(M\) là điểm bất kì thuộc (E). Khi đó, giá trị nhỏ nhất của \(OM\) là:
Đáp án: B Phương pháp giải: - Quan sát đồ thị, dễ dàng nhận thấy rằng OM nhỏ nhất khi M trùng với điểm \((0;\,3)\) hoặc \((0; - 3)\). - Sử dụng phương pháp thế và đánh giá để chứng minh nhận xét trên. Lời giải chi tiết: \(M \in (E) \Rightarrow M({x_0};{y_0}):\,\,\,\,9{x_0}^2 + 16{y_0}^2 = 144 \Leftrightarrow {y_0}^2 = 9 - {9 \over {16}}{x_0}^2\) Ta có: \(O{M^2} = {x_0}^2 + {y_0}^2 = {x_0}^2 + 9 - {9 \over {16}}{x_0}^2 = {7 \over {16}}{x_0}^2 + 9 \ge 9\) \( \Rightarrow OM \ge 3\,\,\,\,\,\, \Rightarrow O{M_{\min }} = 3\) khi và chỉ khi \({x_0} = 0 \Leftrightarrow {y_0} = \pm 3\) Chọn: B Câu hỏi 9 : Cho Elip \((E):\,\,9{x^2} + 25{y^2} = 225\), đường thẳng D qua tiêu điểm \({F_1}\), vuông góc \(Ox\) và cắt (E) tại 2 điểm M và N. Độ dài đoạn thẳng MN = ?
Đáp án: D Phương pháp giải: Đưa phương trình Elip về đúng dạng, xác định các hệ số a, b, c. Viết phương trình đường thẳng D. Giải hệ phương trình để tìm giao điểm của D và (E). Lời giải chi tiết: Ta có: \((E):\,\,9{x^2} + 25{y^2} = 225 \Leftrightarrow {{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1 \Rightarrow a = 5,\,\,b = 3\) Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {3^2} = 16 \Rightarrow c = 4 \Rightarrow \,\,{F_1}( - 4;0)\). Phương trình đường thẳng D qua tiêu điểm \({F_1}\), vuông góc \(Ox\): \(x = - 4\). Tọa độ điểm M, N là nghiệm của hệ phương trình: \(\left\{ \matrix{ 9{x^2} + 25{y^2} = 225 \hfill \cr x = - 4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 4 \hfill \cr 9.{( - 4)^2} + 25.{y^2} = 225 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 4 \hfill \cr y = \pm {9 \over 5} \hfill \cr} \right.\) \( \Rightarrow M\left( { - {9 \over 5}; - 4} \right),\,\,N\left( {{9 \over 5}; - 4} \right) \Rightarrow MN = {{18} \over 5}\) Chọn: D Câu hỏi 10 : Cho elip \((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1\), biết \(M \in (E)\) sao cho \(M{F_1} = 3\). Tọa độ điểm M là:
Đáp án: C Phương pháp giải: Xác định các hệ số a, b, c. Sử dụng công thức \(M{F_1} = a + {c \over a}{x_0}\) Lời giải chi tiết: \((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1 \Rightarrow a = 5,\,\,b = 4\) Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {4^2} = 9 \Rightarrow c = 3\) Gọi \(M\left( {{x_0};{y_0}} \right) \in (E) \Rightarrow {{{x_0}^2} \over {25}} + {{{y_0}^2} \over {16}} = 1\) \(M{F_1} = a + {c \over a}{x_0} = 5 + {3 \over 5}{x_0} = 3 \Rightarrow {x_0} = - {{10} \over 3}\) Ta có: \({{{x_0}^2} \over {25}} + {{{y_0}^2} \over {16}} = 1 \Leftrightarrow {{{{\left( { - {{10} \over 3}} \right)}^2}} \over {25}} + {{{y_0}^2} \over {16}} = 1 \Leftrightarrow {y_0}^2 = {{80} \over 9} \Leftrightarrow {y_0} = \pm {{4\sqrt 5 } \over 3}\) Vậy, \(M\left( { - {{10} \over 3}; - {{4\sqrt 5 } \over 3}} \right)\) hoặc \(M\left( { - {{10} \over 3};{{4\sqrt 5 } \over 3}} \right)\). Chọn: C Câu hỏi 11 : Cho Elip \((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\). Xác định tọa độ điểm \(M \in (E)\) thỏa mãn: \(M{F_1} - M{F_2} = 2\).
Đáp án: D Phương pháp giải: Xác định các hệ số a, b, c. \(M{F_1} + M{F_2} = 2a,\,\,\,M{F_1} = a + {c \over a}{x_0},\,\,\,M{F_2} = a - {c \over a}{x_0}\) Lời giải chi tiết: \((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1 \Rightarrow a = 5,\,\,b = 3\) Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {3^2} = 16 \Rightarrow c = 4\). Gọi \(M\left( {{x_0};{y_0}} \right) \in (E) \Rightarrow \,{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1\) \(M{F_1} + M{F_2} = 2.5 = 10\) Theo đề bài, ta có: \(M{F_1} - M{F_2} = 2 \Rightarrow \left\{ \matrix{ M{F_1} = {{10 + 2} \over 2} = 6 \hfill \cr M{F_2} = {{10 - 2} \over 2} = 4 \hfill \cr} \right.\) \(M{F_1} = a + {c \over a}{x_0} = 5 + {4 \over 5}{x_0} = 6 \Rightarrow {x_0} = {5 \over 4}\) Mà \(\,{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1 \Rightarrow {{{{\left( {{5 \over 4}} \right)}^2}} \over {25}} + {{{y_0}^2} \over 9} = 1 \Leftrightarrow {y_0} = \pm {{3\sqrt {15} } \over 4}\) Vậy \(M\left( {{5 \over 4}; - {{3\sqrt {15} } \over 4}} \right)\) hoặc \(M\left( {{5 \over 4};{{3\sqrt {15} } \over 4}} \right)\). Chọn: D Câu hỏi 12 : Cho elip \((E):\,\,{{{x^2}} \over {16}} + {{{y^2}} \over 7} = 1\), điểm\(M \in (E)\), nằm trong góc phần tư thứ (III) và có bán kính qua tiêu bằng \({5 \over 2}\) có tọa độ là:
Đáp án: A Phương pháp giải: Xác định các hệ số a, b, c. Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc góc phần tư thứ (III) \( \Leftrightarrow \left\{ \matrix{ {x_0} < 0 \hfill \cr {y_0} < 0 \hfill \cr} \right.\) Bán kính qua tiêu bằng \({5 \over 2} \Leftrightarrow \left[ \matrix{ M{F_1} = {5 \over 2} \hfill \cr M{F_2} = {5 \over 2} \hfill \cr} \right.\) Sử dụng các công thức \(M{F_1} = a + {c \over a}{x_0};\,\,M{F_2} = a - {c \over a}{x_0}\) Lời giải chi tiết: \((E):\,\,{{{x^2}} \over {16}} + {{{y^2}} \over 7} = 1 \Rightarrow a = 4,\,\,b = \sqrt 7 \) Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {4^2} - {\left( {\sqrt 7 } \right)^2} = 9 \Rightarrow c = 3\). Gọi \(M\left( {{x_0};{y_0}} \right) \in (E) \Rightarrow {{{x_0}^2} \over {16}} + {{{y_0}^2} \over 7} = 1\) \(M\) nằm trong góc phần tư thứ (III) \( \Leftrightarrow {x_0} < 0,\,\,\,\,{y_0} < 0\) Theo đề bài, ta có: \(\left[ \matrix{ M{F_1} = {5 \over 2} \Leftrightarrow a + {c \over a}{x_0} = {5 \over 2} \Leftrightarrow 4 + {3 \over 4}{x_0} = {5 \over 2} \Leftrightarrow {x_0} = - 2\,\,\left( {tm} \right) \hfill \cr M{F_2} = {5 \over 2} \Leftrightarrow a - {c \over a}{x_0} = {5 \over 2} \Leftrightarrow 4 - {3 \over 4}{x_0} = {5 \over 2} \Leftrightarrow {x_0} = 2\,\,\left( {ktm} \right) \hfill \cr} \right.\) Mà \({{{x_0}^2} \over {16}} + {{{y_0}^2} \over 7} = 1 \Rightarrow {{{{( - 2)}^2}} \over {16}} + {{{y_0}^2} \over 7} = 1 \Leftrightarrow \left[ \matrix{ {y_0} = {{\sqrt {21} } \over 2}\,\,\,\,\,\,\,\,\left( {ktm} \right) \hfill \cr {y_0} = - {{\sqrt {21} } \over 2}\,\,\,\,\left( {tm} \right) \hfill \cr} \right.\) Vậy, \(M\left( { - 2; - {{\sqrt {21} } \over 2}} \right)\) Chọn: A Câu hỏi 13 : Cho elip \((E):\,\,\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\). Trong các điểm sau, điểm nào là tiêu điểm của \((E)\)?
Đáp án: D Phương pháp giải: \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) Sử dụng công thức \({a^2} - {b^2} = {c^2}\) tính c. Từ đó, kết luận tiêu điểm của (E) là \({F_1}( - c;0),\,\,{F_2}(c;0)\). Lời giải chi tiết: \((E):\,\,\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1 \Rightarrow a = 10,\,\,b = 6\) Mà \({a^2} - {b^2} = {c^2} \Leftrightarrow {c^2} = {10^2} - {6^2} = 64 \Rightarrow c = 8 \Rightarrow {F_1}( - 8;0),\,\,{F_2}(8;0)\) Chọn: D Câu hỏi 14 : Cho elip \((E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tâm sai và tiêu cự của (E) là:
Đáp án: C Phương pháp giải: \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) Sử dụng công thức \({a^2} - {b^2} = {c^2}\) tính tiêu cự c. Tính tâm sai \(e = \frac{c}{a}\). Lời giải chi tiết: \((E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1 \Rightarrow a = 5,\,\,b = 4\) Mà \({a^2} - {b^2} = {c^2} \Leftrightarrow {c^2} = {5^2} - {4^2} = 9 \Rightarrow c = 3\) Tâm sai \(e = \frac{c}{a} = \frac{3}{5}\) Chọn: C Câu hỏi 15 : Trong mặt phẳng với hệ tọa độ \(Oxy,\) cho elíp \((E)\) có phương trình chính tắc là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Tiêu cự của \((E)\) là
Đáp án: A Phương pháp giải: Tiêu cự của elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \(2c = 2\sqrt {{a^2} - {b^2}} .\) Lời giải chi tiết: Tiêu cự của \(\left( E \right)\) là \(2\sqrt {25 - 9} = 2.\sqrt {16} = 2.4 = 8\) Chọn A. Câu hỏi 16 : Trong mặt phẳng \(Oxy\), phương trình nào sau đây là phương trình chính tắc của một elip?
Đáp án: D Phương pháp giải: Phương trình chính tắc của Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({a^2} - {b^2} = {c^2}\,\,(a > b)\) Lời giải chi tiết: Phương trình \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\) là phương trình chính tắc của 1 Elip Chọn D. Câu hỏi 17 : \(\left( E \right):\,\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1\) có tâm sai \(e\) là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Ta có: \(a = 5,\,\,b = 4 \Rightarrow {c^2} = {a^2} - {b^2} = 9 \Rightarrow c = 3\). \( \Rightarrow e = \dfrac{c}{a} = \dfrac{3}{5}\). Chọn B. Câu hỏi 18 : \(\left( E \right):\,\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\) có tiêu điểm \({F_2}\) là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: \(*\,\,a = 4,\,\,b = 3 \Rightarrow {c^2} = {a^2} - {b^2} = 7 \Rightarrow c = \sqrt 7 \). * Ta có \({F_2}\left( {c;0} \right) \Rightarrow {F_2}\left( {\sqrt 7 ;0} \right)\). Chọn C. Câu hỏi 19 : Đường Elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) có tiêu cự bằng:
Đáp án: A Phương pháp giải: Tiêu cự của elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \(2c = 2\sqrt {{a^2} - {b^2}} .\) Lời giải chi tiết: Đường Elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) có tiêu cự bằng \(2\sqrt {16 - 7} = 2\sqrt 9 = 6\) Chọn A. Câu hỏi 20 : Trong các phương trình sau, phương trình nào là phương trình chính tắc của Elip?
Đáp án: C Phương pháp giải: Với \({F_1}\left( { - c;\,\,0} \right),\,\,{F_2}\left( {c;\,\,0} \right)\) ta có: \(M\left( {x;y} \right) \in \left( E \right) \Leftrightarrow \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,\left( 1 \right)\) trong đó \({b^2} = {a^2} - {c^2}\) Phương trình \(\left( 1 \right)\) được gọi là phương trình chính tắc của elip \(\left( E \right)\). Lời giải chi tiết: Phương trình \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\) được viết dưới dạng \(\frac{{{x^2}}}{{{3^3}}} + \frac{{{y^2}}}{{{4^2}}} = 1\) (là dạng phương trình chính tắc của Elip) Phương trình chính tắc của Elip là: \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\) Chọn C. Câu hỏi 21 : Một tiêu điểm của Elip \(\left( E \right):\,\,\frac{{{x^2}}}{9} + \frac{{{y^2}}}{6} = 1\) có tọa độ là:
Đáp án: D Phương pháp giải: Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {c^2} = {a^2} - {b^2}\) \( \Rightarrow \)Tiêu điểm của elip là \({F_1}\left( {c;\,\,0} \right),\,\,{F_2}\left( { - c;\,\,0} \right)\). Lời giải chi tiết: Xét Elip \(\left( E \right):\,\,\,\frac{{{x^2}}}{9} + \frac{{{y^2}}}{6} = 1\) ta có: \(\left\{ \begin{array}{l}{a^2} = 9\\{b^2} = 6\end{array} \right. \Rightarrow {c^2} = {a^2} - {b^2} = 9 - 6 = 3 \Rightarrow c = \sqrt 3 \) \( \Rightarrow \) Elip \(\left( E \right)\) có hai tiêu điểm là \({F_1}\left( { - \sqrt 3 ;\,\,0} \right)\) và \({F_2}\left( {\sqrt 3 ;\,\,0} \right)\). Chọn D. Câu hỏi 22 : Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) có độ dài trục lớn bằng:
Đáp án: B Phương pháp giải: Phương trình chính tắc của Elip \(\left( E \right)\) là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), có độ dài trục lớn là \({A_1}{A_2} = 2a\). Lời giải chi tiết: Xét Elip \(\left( E \right):\,\,\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) ta có: \(\left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 5\\b = 3\end{array} \right.\) Độ dài trục lớn là: \({A_1}{A_2} = 2.\,5 = 10\) Vậy độ dài trục lớn của Elip \(\left( E \right)\) là \(10.\) Chọn B. Câu hỏi 23 : Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) có tâm sai bằng bao nhiêu?
Đáp án: A Phương pháp giải: \(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tâm sai \(e = \frac{c}{a}\). Lời giải chi tiết: Xét Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) ta có: \(\left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right. \Rightarrow {c^2} = {a^2} - {b^2} = 25 - 9 = 16\)\( \Rightarrow c = 4\) (Do \(c > 0\)) Vậy tâm sai của elip \(\left( E \right)\) là \(e = \frac{c}{a} = \frac{4}{5} \cdot \) Chọn A. Câu hỏi 24 : Cho elip có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 6\). Khi đó, tọa độ tiêu điểm của elip là:
Đáp án: A Phương pháp giải: Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {c^2} = {a^2} - {b^2}\) \( \Rightarrow \)Tiêu điểm của elip là \({F_1}\left( {c;\,\,0} \right),\,\,{F_2}\left( { - c;\,\,0} \right).\) Lời giải chi tiết: Xét elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 6,\) ta có: \(\left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 9\end{array} \right. \Rightarrow {c^2} = {a^2} - {b^2} \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt 7 \) Vậy elip có hai tiêu điểm là \({F_1}\left( { - \sqrt 7 ;\,\,0} \right),\,\,{F_2}\left( {\sqrt 7 ;\,\,0} \right).\) Chọn A. Câu hỏi 25 : Trong mặt phẳng tọa độ Oxy, cho elip \(\left( E \right):\,\,{\mkern 1mu} {\mkern 1mu} \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Tiêu cự của elip \(\left( E \right)\)
Đáp án: B Phương pháp giải: Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu cự \(2c\) với \(c = \sqrt {{a^2} - {b^2}} \). Lời giải chi tiết: \(\begin{array}{l}\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\\ \Rightarrow {a^2} = 25,\,\,\,{b^2} = 9\\ \Rightarrow {c^2} = {a^2} - {b^2} = 25 - 9 = 16\\ \Rightarrow c = 4\end{array}\) Vậy tiêu cự là \(2c = 2.4 = 8\). Chọn B.
|