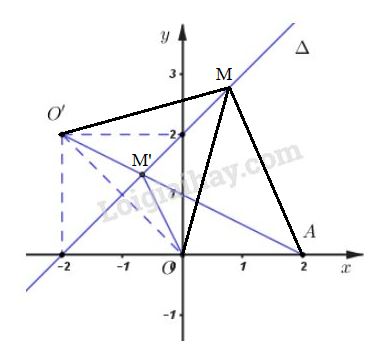
Bài 4 trang 93 SGK Hình học 10

LG a

Tìm điểm đối xứng của $O$ qua $Δ$

Lời giải chi tiết:

Gọi $H(x;y)$ là hình chiếu của $O$ trên $Δ$, $\overrightarrow {OH}  = (x;y)$

$Δ: x – y + 2 = 0$ có vecto chỉ phương $\overrightarrow u (1;1)$

$\overrightarrow {OH}  \bot \Delta$ $\Rightarrow 1.x + 1.y = 0 \Leftrightarrow x + y = 0$

Tọa độ điểm $H$ là nghiệm của hệ phương trình:

$\left\{ \matrix{ x + y = 0 \hfill \cr  x - y + 2 = 0 \hfill \cr} \right. \Rightarrow H( - 1;1)$

Gọi $O’$ là đỉnh đối xứng của $O$ qua $Δ$ thì $H$ là trung điểm của đoạn thẳng $OO’$

$\eqalign{ & {x_H} = {{{x_O} + {x_{O'}}} \over 2} \Leftrightarrow - 1 = {{0 + {x_{O'}}} \over 2} \cr&\Rightarrow {x_{O'}} = - 2 \cr  & {y_H} = {{{y_O} + {y_{O'}}} \over 2} \Leftrightarrow - 1 = {{0 + {y_{O'}}} \over 2}\cr& \Rightarrow {y_{O'}} = 2 \cr}$

Vậy $O’(-2;2)$.

Cách khác:

Gọi $d$ là đường thẳng đi qua $O$ và vuông góc $\Delta$.

$\Delta$ nhận $\overrightarrow n  = \left( {1; - 1} \right)$ làm VTPT nên nhận $\overrightarrow u  = \left( {1;1} \right)$ làm VTCP.

$d \bot \Delta  \Rightarrow \overrightarrow {{n_d}}  = \overrightarrow u  = \left( {1;1} \right)$ là VTPT của $d$.

Mà $d$ đi qua $O\left( {0;0} \right)$ nên $1\left( {x - 0} \right) + 1\left( {y - 0} \right) = 0$ $\Leftrightarrow x + y = 0$

Gọi $H = d \cap \Delta$ thì tọa độ điểm $H$ thỏa mãn:

$\left\{ \begin{array}{l}x + y = 0\\x - y + 2 = 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 1\end{array} \right.$ $\Rightarrow H\left( { - 1;1} \right)$

$O'$ đối xứng $O$ qua $\Delta$ hay $H$ là trung điểm $OO'$

$\Leftrightarrow \left\{ \begin{array}{l}{x_{O'}} = 2{x_H} - {x_O} = 2.\left( { - 1} \right) - 0 =  - 2\\{y_{O'}} = 2{y_H} - {y_O} = 2.1 - 0 = 2\end{array} \right.$

$\Rightarrow O'\left( { - 2;2} \right)$.

LG b

Tìm điểm $M$ trên $Δ$ sao cho độ dài đường gấp khúc $OMA$ ngắn nhất.

Lời giải chi tiết:

Quan sát hình vẽ ta thấy,

$A$ và $O$ nằm cùng phía so với $\Delta$ hay $A,O'$ nằm khác phía so với $\Delta$.

Gọi $M' = AO' \cap \Delta$ thì $OM' = O'M'$ do $\Delta$ là đường trung trực của $OO'$.

Với điểm $M$ bất kì thuộc $\Delta$ thì $OM + AM = O'M + AM \ge O'A$

$\Rightarrow {\left( {OM + MA} \right)_{\min }} = AO'$ khi $M \equiv M'$ là giao điểm của $AO'$ với $\Delta$.

$A(2; 0); O'(-2; 2)$ $\Rightarrow \overrightarrow {AO'}  = \left( { - 4;2} \right)$ là VTCP của $AO'$ $\Rightarrow \overrightarrow {{n_{AO'}}}  = \left( {2;4} \right)$ là VTPT của $AO'$

Mà $AO'$ đi qua $A\left( {2;0} \right)$ nên $2\left( {x - 2} \right) + 4\left( {y - 0} \right) = 0$ $\Leftrightarrow 2x + 4y - 4 = 0$ $\Leftrightarrow x + 2y - 2 = 0$

$M = AO' \cap \Delta$ $\Leftrightarrow \left\{ \begin{array}{l}x + 2y - 2 = 0\\x - y + 2 = 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x =  - \dfrac{2}{3}\\y = \dfrac{4}{3}\end{array} \right.$

Vậy $M\left( { - \dfrac{2}{3};\dfrac{4}{3}} \right)$

HocTot.Nam.Name.Vn