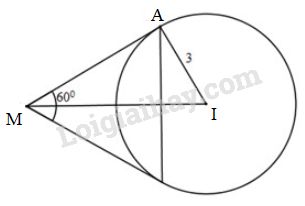
Bài 7 trang 93 SGK Hình học 10Cho đường tròn (C) có tâm I(1, 2) và bán kính bằng 3. Chứng minh rằng tập hợp các điểm M từ đó ta sẽ được hai tiếp tuyến với (C) tạo với nhau một góc 600 là một đường tròn. Đề bài Cho đường tròn \((C)\) có tâm \(I(1; 2)\) và bán kính bằng \(3\). Chứng minh rằng tập hợp các điểm \(M\) từ đó ta sẽ được hai tiếp tuyến với \((C)\) tạo với nhau một góc \(60^0\) là một đường tròn. Hãy viết phương trình đường tròn đó. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Tính khoảng cách MI dựa vào tỉ số lượng giác của góc nhọn trong tam giác AMI. Từ đó suy ra quỹ tích cần tìm. Lời giải chi tiết Theo tính chất của tiếp tuyến cắt nhau ta có \(\displaystyle MI\) là tia phân giác góc \(\displaystyle M\) \(\displaystyle \Rightarrow \) \(\displaystyle \widehat {AMI} = {30^0}\) Tam giác \(\displaystyle IAM\) vuông tại \(\displaystyle A\) (vì \(IA \bot MA\)) có: \(\displaystyle \sin \widehat {AMI} = \frac{{IA}}{{IM}} \Rightarrow IM = {{IA} \over {\sin \widehat {AMI}}} \) \(\displaystyle = {3 \over {\sin {{30}^0}}} = {3 \over {{1 \over 2}}} = 6\) \(\displaystyle \Rightarrow \) \(\displaystyle M\) luôn cách \(\displaystyle I\) cố định một khoảng bằng \(\displaystyle 6\). Vậy quỹ tích \(\displaystyle M\) là đường tròn tâm \(\displaystyle I (1; 2)\), bán kính \(\displaystyle R = 6\) Phương trình đường tròn là: \(\displaystyle {(x - 1)^2} + {(y - 2)^2} = 36\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
