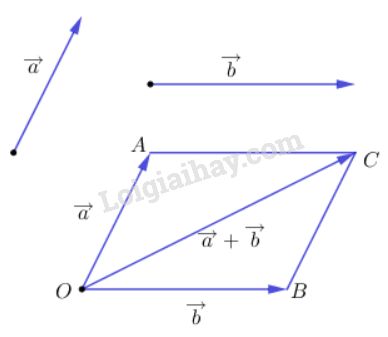
Bài 4 trang 27 SGK Hình học 10

Đề bài

Chứng minh rằng \(|\overrightarrow a  + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} .\)

Lời giải chi tiết

Từ một điểm \(O\) trong mặt phẳng ta dựng vectơ:

\(\eqalign{
& \overrightarrow {OA} = \overrightarrow a \cr 
& \overrightarrow {OB} = \overrightarrow b \cr} \)

Và dựng hình bình hành \(OACB\) \( \Rightarrow \overrightarrow {AC}  = \overrightarrow {OB} \)

Như vậy:

\(\eqalign{
& OA = |\overrightarrow {OA} | = |\overrightarrow a | \cr
& OB = |\overrightarrow {OB} | = |\overrightarrow b | \cr&\Rightarrow AC = |\overrightarrow {AC} |=|\overrightarrow {OB} |  = |\overrightarrow b | \cr
& \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \Rightarrow \overrightarrow {OC} = \overrightarrow a + \overrightarrow b \cr
& OC = |\overrightarrow {OC} | = |\overrightarrow a + \overrightarrow b | \cr} \)

Áp dụng bất đẳng thức tam giác vào tam giác \(OAC\), ta có:

\(OA + AC ≥ OC \) \(\Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \ge \left| {\overrightarrow a  + \overrightarrow b } \right|\)

\(   ⇒ |\overrightarrow a  + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} \).

Dấu "=" xảy ra khi OA+AC=OC hay A nằm giữa O và C.

Khi đó \(\overrightarrow {OA} ,\overrightarrow {AC} \) cùng hướng hay \(\overrightarrow a ,\overrightarrow b \) cùng hướng. (Do \(\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {AC}  = \overrightarrow b \))

Chú ý:

Các em cũng không nhất thiết phải dựng hình bình hành. Có thể dựng hình cách khác như sau:

Từ điểm O dựng điểm A sao cho \(\overrightarrow {OA}  = \overrightarrow a \).

Từ điểm A dựng điểm C sao cho \(\overrightarrow {AC}  = \overrightarrow b \).

Rồi sử dụng bất đẳng thức tam giác cũng ra được đpcm.

HocTot.Nam.Name.Vn