Bài 5 trang 27 (Ôn tập chương I - Vectơ) SGK Hình học 10Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho: Video hướng dẫn giải Cho tam giác đều ABCABC nội tiếp đường tròn tâm OO. Hãy xác định các điểm M,N,PM,N,P sao cho: LG a →OM=→OA+→OB−−→OM=−−→OA+−−→OB Lời giải chi tiết:
Kéo dài OCOC cắt đường tròn tại điểm MM. MC là đường kính nên ^MBC=900⇒MB⊥BCˆMBC=900⇒MB⊥BC. Mà tam giác ABC đều nên AO⊥BCAO⊥BC. Do đó MB//OA (1) Lại có ^MAC=900⇒MA⊥ACˆMAC=900⇒MA⊥AC. Mà tam giác ABC đều nên BO⊥ACBO⊥AC. Do đó MA//BO (2) Từ (1) và (2) suy ra OAMBOAMB là hình bình hành, suy ra: →OA+→OB=→OM−−→OA+−−→OB=−−→OM. Vậy M là điểm cần tìm. Cách 2: O là tâm tam giác ABC nên cũng là trọng tâm tam giác. Ta có: →OA+→OB+→OC=→0⇔→OA+→OB=−→OC Mà →OM=→OA+→OB Nên →OM=−→OC ⇒→OM là véc tơ đối của →OC hay O là trung điểm của CM. Mà OC là bán kính nên CM=2CO là đường kính của đường tròn. Vậy M là giao điểm của CO với đường tròn. Cách 3: →OM=→OA+→OB ⇔ M là đỉnh còn lại của hình bình hành AOBM. + AOBM là hình bình hành ⇒ AM = OB Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1) + AOBM là hình bình hành ⇒ AM//BO ⇒^MAO+^AOB=1800⇔^MAO+1200=1800⇒^MAO=600(2) Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC. Mà ^AOM=^BOM nên M là điểm chính giữa cung AB. LG b →ON=→OB+→OC Lời giải chi tiết: Nối OA và kéo dài cắt đường tròn tại điểm N Tương tự như trên ta có: →ON=→OB+→OC Cách khác: →ON=→OB+→OC ⇔ N là đỉnh còn lại của hình bình hành BOCN. + BOCN là hình bình hành ⇒ OB=CN Mà OB = OC (= bán kính đường tròn) ⇒ CN = CO ⇒ ΔCNO cân tại C (1) + BOCN là hình bình hành ⇒ CN//BO ⇒^NCO+^BOC=1800⇔^NCO+1200=1800⇒^NCO=600(2) Từ (1) và (2) ⇒ ΔCNO đều ⇒ ON = OC ⇒ N nằm trên đường tròn ngoại tiếp ΔABC. Mà ^BON=^CON nên N là điểm chính giữa cung BC. LG c →OP=→OC+→OA Lời giải chi tiết: Nối OB và kéo dài cắt đường tròn tại điểm P Tương tự như trên ta có: →OP=→OC+→OA Cách khác: →OP=→OC+→OA ⇔ P là đỉnh còn lại của hình bình hành AOCP. + AOCP là hình bình hành ⇒ OA=PC Mà OA = OC (= bán kính đường tròn) ⇒ OC = PC ⇒ ΔCPO cân tại C (1) + AOCP là hình bình hành ⇒ AO//CP ⇒^PCO+^COA=1800⇔^PCO+1200=1800⇒^PCO=600(2) Từ (1) và (2) ⇒ ΔCPO đều ⇒ OP = OC ⇒ P nằm trên đường tròn ngoại tiếp ΔABC. Mà ^AOP=^COP nên P là điểm chính giữa cung AC. HocTot.Nam.Name.Vn
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|













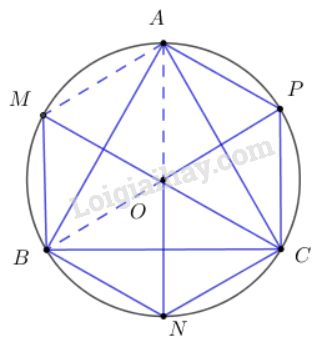 Cách 1:
Cách 1:







