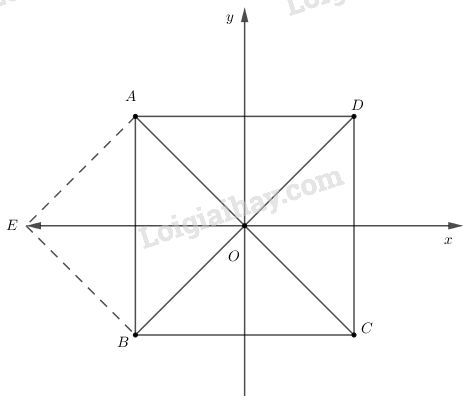
Bài 15 trang 30 SGK Hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ.

Khẳng định nào sau đây là đúng?

A) \(|\overrightarrow {OA}  + \overrightarrow {OB} | = AB\)

B) \(\overrightarrow {OA}  - \overrightarrow {OB} \) và \(\overrightarrow {DC}\) cùng hướng

C) \({x_A} =  - {x_C}\) và \({y_A} = {y_C}.\)

D) \({x_B} =  - {x_C}\) và \({y_C} =- {y_B}.\)

Lời giải chi tiết

A) Ta có: 

\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CO} + \overrightarrow {OB} = \overrightarrow {CB} \\
\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {CB} } \right| = CB = AB
\end{array}\)

A đúng.

B) Vì \(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {BA} \)

Mà \(\overrightarrow {BA} \) và \(\overrightarrow {DC} \) ngược hướng nên B) sai

C) Vì \({x_A} =  - {x_C},\;\;y{ _A} =  - {y_C} \Rightarrow C\) sai.

D) Vì \({x_B} =  - {x_C},\;\;{y_B} = {y_C} \Rightarrow D\) sai.

Chọn A.

Cách giải thích khác:

Qua A kẻ \(\overrightarrow {AE}  = \overrightarrow {OB} \)\( \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OA}  + \overrightarrow {AE}\)\(  = \overrightarrow {OE} \)

Ta dễ dàng chứng minh được:

 \(\overrightarrow {OE}  = \overrightarrow {DA}  \Rightarrow |\overrightarrow {OA}  + \overrightarrow {OB} |= |\overrightarrow {OE} |\)\( =|\overrightarrow {DA} |= |\overrightarrow {BA} | = AB\)

Vậy A) đúng.

HocTot.Nam.Name.Vn