Đồ thị hàm số bậc ba luôn

Tập xác định của hàm số $y = - \dfrac{1}{2}{x^3} + 2x - 1$ là:

Hàm đa thức bậc ba có thể có mấy cực trị?

Hàm đa thức bậc ba không có cực trị và nghịch biến có bảng biến thiên dạng nào dưới đây?

Cho bảng biến thiên hình bên, hàm số nghịch biến trên:

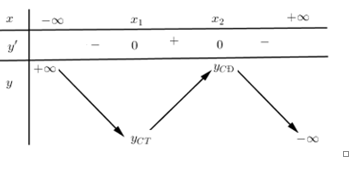
Đồ thị hàm số bậc ba có mấy tâm đối xứng?

Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:

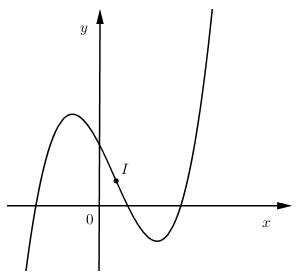
Chọn kết luận đúng:

Nếu điểm cực đại của đồ thị hàm số bậc ba nằm ở trục hoành thì:

Nếu điểm cực tiểu của đồ thị hàm số bậc ba nằm ở trục hoành thì đồ thị hàm số có mấy điểm chung với $Ox$?

Cho hàm số $y = f\left( x \right)$ có hai cực trị thỏa mãn ${y_{CD}}.{y_{CT}} < 0$. Khi đó:

Cho hàm số bậc ba $y = f\left( x \right)$ có hai điểm cực trị thỏa mãn ${y_{CD}}.{y_{CT}} > 0$. Khi đó, đồ thị hàm số có mấy điểm chung với trục $Ox$?

Chọn kết luận đúng: