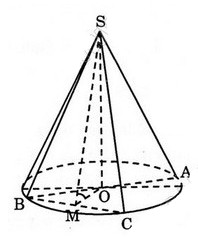
Giải bài 9 trang 40 SGK Hình học lớp 12

LG a

a) Tính diện tích xuang quanh, diện tích đáy và thể tích của khối nón tương ứng.

Phương pháp giải:

+) Cắt hình nón đỉnh \(S\) bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền chính là đường kính của đường tròn đáy của hình nón. Từ đó suy ra bán kính đáy \(r\) của hình nón.

+) Độ dài đường sinh \(l\) của hình nón chính là cạnh góc vuông của tam giác vuông cân.

+) Áp dụng công thức \(h = \sqrt {{l^2} - {r^2}} \), tính độ dài đường cao của hình nón.

+) Tính diện tích xung quanh \({S_{xq}} = \pi rl\), diện tích đáy \({S_đ} = \pi {r^2}\) và thể tích của khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

a) Tam giác \(SAB\) vuông cân tại S nên \(SA = SB = a\).

Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy \(r = \dfrac{a\sqrt{2}}{2}\), đường sinh \(l = a\).

Gọi \(h\) là độ dài đường cao của hình nón ta có: \(h = \sqrt {{l^2} - {r^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 2 }}{2}\)

Vậy \(S_{xq} = πrl =\) \( \dfrac{\sqrt{2}}{2}\pi a^2\) ( đơn vị diện tích)

\(S_{đáy}\) = \( \pi r^{2}\) = \( \pi \dfrac{a^{2}}{2}\) ( đơn vị diện tích);

\(V\)nón = \( \dfrac{1}{3}\pi r^{2}h\) \( = \dfrac{\sqrt{2}}{12}\pi a^{3}\) (đơn vị thể tích)

LG b

b) Cho một dây cung \(BC\) của đường tròn đáy hình nón sao cho mặt phẳng \((SBC)\) tạo với mặt phẳng chứa đáy hình nón một góc \(60^0\). Tính diện tích tam giác \(SBC\).

Phương pháp giải:

Xác định góc giữa (SBC) và mặt đáy.

Nhận xét \(\Delta SBC\) là tam giác cân, hạ đường cao \(SM\) của tam giác cân đó thì \(M\) là trung điểm của \(BC\).

+) Dựa vào định lí Pitago tính \(SM\) và \(BC\).

+) \({S_{\Delta SBC}} = \dfrac{1}{2}SM.BC\)

Lời giải chi tiết:

Gọi tâm đáy là \(O\) và trung điểm cạnh \(BC\) là \(M\) ta có: \({OM \bot BC}\) (quan hệ vuông góc giữa đường kính và dây cung).

Ta có:

\[\begin{array}{l}
\left\{ \begin{array}{l}
BC \bot OM\\
BC \bot SO
\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right) \Rightarrow BC \bot SM\\
\left\{ \begin{array}{l}
\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\
SM \bot BC\\
OM \bot BC
\end{array} \right. \\\Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;OM} \right)} = \widehat {SMO} = {60^0}
\end{array}\]

Ta có: \(SM = \dfrac{{SO}}{{\sin 60}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{a\sqrt 6 }}{3}\).

\(OM = SO.\cot 60 = \dfrac{{a\sqrt 2 }}{2}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}\)

Ta có \(∆ OMB\) vuông ở \(M\) nên \( BM^{2}= BO^{2} - OM^{2} = \dfrac{a^{2}}{3}\)

Vậy \(BM =  \dfrac{a}{\sqrt{3}}\Rightarrow BC =2BM=  \dfrac{2a}{\sqrt{3}}\)

Do đó \(S = {{SM.BC}\over2}\) = \( \dfrac{\sqrt{2}}{3}a^{2}\) (đơn vị diện tích).

HocTot.Nam.Name.Vn