Giải bài 7 trang 39 SGK Hình học lớp 12

LG a

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

Phương pháp giải:

Áp dụng công thức: ${S_{xq}} = 2\pi rh,\,\,{S_{tp}} = 2\pi rh + \pi {r^2}$ với $r;h$ lần lượt là bán kính đáy và độ dài đường cao của hình trụ.

Lời giải chi tiết:

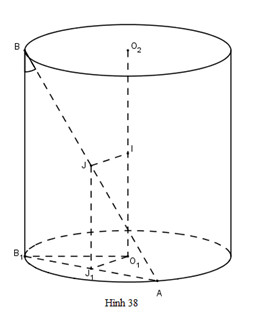
Theo công thức ta có:

$S_{xq} = 2πrh = 2\sqrt3 πr^2$ 

$S_{tp} = 2πrh + 2πr^2 =  2\sqrt3 πr^2 + 2 πr^2$

$= 2(\sqrt3 + 1)πr^2$  ( đơn vị thể tích)

LG b

b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.

Phương pháp giải:

Áp dụng công thức: $V = \pi {r^2}h$.

Lời giải chi tiết:

$V$trụ = $πR^2h = \sqrt3 π r^3$

LG c

c) Cho hai điểm $A$ và $B$ lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng $AB$ và trục của hình trụ bằng $30^0$. Tính khoảng cách giữa đường thẳng $AB$ và trục của hình trụ.

Phương pháp giải:

+) Giả sử trục của hình trụ là $O_1O_2$ và $A$ nằm trên đường tròn tâm $O_1$, $B$ nằm trên đường tròn tâm $O_2$. Kẻ $BB_1$ // ${O_1}{O_2}$ $\Rightarrow \widehat {\left( {AB;{O_1}{O_2}} \right)} = \widehat {\left( {AB;B{B_1}} \right)} = \widehat {AB{B_1}}$.

+) Xác định khoảng cách giữa AB và ${O_1}{O_2}$ bằng cách xác định đường vuông góc chung giữa hai đường thẳng đó.

Lời giải chi tiết:

Giả sử trục của hình trụ là $O_1O_2$ và $A$ nằm trên đường tròn tâm $O_1$, $B$ nằm trên đường tròn tâm $O_2$; $I$ là trung điểm của $O_1O_2$ , $J$ là trung điểm của $AB$.

Ta chứng minh $IJ$ là đường vuông góc chung của $O_1O_2$  và $AB$.

Hạ $BB_1$ vuông góc với đáy, $J_1$ là hình chiếu vuông góc của $J$ xuống đáy.

Dễ thấy $J_1$ là trung điểm của $AB_1$ (định lí đường trung bình của tam giác).

Ta có: $\left\{ \begin{array}{l}{O_1}{J_1} \bot A{B_1}\\{O_1}{J_1} \bot B{B_1}\end{array} \right. \Rightarrow {O_1}{J_1} \bot \left( {AB{B_1}} \right)$.

Mà $IJ//{O_1}{J_1} \Rightarrow IJ \bot \left( {AB{B_1}} \right)$ $\Rightarrow IJ \bot AB$.

$\left\{ \begin{array}{l}IJ//{O_1}{J_1}\\{O_1}{O_2} \bot {O_1}{J_1}\end{array} \right. \Rightarrow IJ \bot {O_1}{O_2}$.

Vậy IJ là đường vuông góc chung của $O_1O_2$  và $AB$ $\Rightarrow d\left( {AB;{O_1}{O_2}} \right) = IJ$

Ta có: $BB_1$ // ${O_1}{O_2}$ $\Rightarrow \widehat {\left( {AB;{O_1}{O_2}} \right)} = \widehat {\left( {AB;B{B_1}} \right)} = \widehat {AB{B_1}}$.

do vậy: $AB_1 = BB_1.tan 30^0$ = $\frac{\sqrt{3}}{3}h = r$.

Xét tam giác vuông $O_1J_1A$ vuông tại $J_1$ ta có: 

$O_{1}J^{2}_{1}$ = $O_{1}A^{2}$ - $AJ^{2}_{1} =$ $r^{2} - {\left( {{r \over 2}} \right)^2}=$ $\frac{3}{4}r^{2}$ $\Rightarrow {O_1}{J_1} = \frac{{r\sqrt 3 }}{2}$

Vậy khoảng cách giữa $AB$ và $O_1O_2$ là: $\frac{\sqrt{3}}{2}r$.

HocTot.Nam.Name.Vn