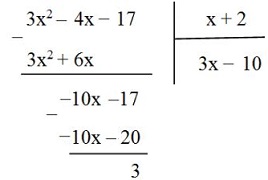Bài 63 trang 62 SGK Toán 8 tập 1

LG a.

\(\dfrac{{3{x^2} - 4x - 17}}{{x + 2}}\);

Phương pháp giải:

Để giá trị của phân thức là số nguyên thì tử thức chia hết cho mẫu thức.

Lời giải chi tiết:

Ta có:

Do đó:  \(\dfrac{{3{x^2} - 4x - 17}}{{x + 2}} = 3x - 10 + \dfrac{3}{{x + 2}}\) 

Để phân thức là số nguyên thì \( \dfrac{3}{{x + 2}}\) phải là số nguyên (với giá trị nguyên của \(x\)).

\( \dfrac{3}{{x + 2}}\) nguyên thì \(x +2\) phải là ước của \(3.\)

Các ước của \(3\) là  \( \pm 1, \pm 3\) . Do đó \( x+2 \in \{ -3; \; -1;\; 1; \;3\}\).

Ta có bảng sau: 

Vậy \(x \in  \{- 5; \;- 3;\; - 1;\; 1\}.\)

Cách khác:

\(\eqalign{
& {{3{x^2} - 4x - 17} \over {x + 2}} \cr 
& = {{\left( {3{x^2} + 6x} \right) - \left( {10x + 20} \right) + 3} \over {x + 2}} \cr 
& = {{3x\left( {x + 2} \right) - 10\left( {x + 2} \right) + 3} \over {x + 2}} \cr& = {{(3x-10)\left( {x + 2} \right)+3} \over {x + 2}}\cr & = {{(3x-10)\left( {x + 2} \right)} \over {x + 2}}+{3\over x+2} \cr 
& = 3x - 10 + {3 \over {x + 2}} \cr} \)

Rồi làm tiếp tục như trên ta được kết quả \(x \in  \{- 5; \;- 3;\; - 1;\; 1\}.\)

LG b.

\(\dfrac{{{x^2} - x + 2}}{{x - 3}}\)

Phương pháp giải:

Để giá trị của phân thức là số nguyên thì tử thức chia hết cho mẫu thức.

Lời giải chi tiết:

Ta có:

\(\eqalign{
& {{{x^2} - x + 2} \over {x - 3}} \cr 
& = {{\left( {{x^2} - 3x} \right) + \left( {2x - 6} \right) + 8} \over {x - 3}} \cr 
& = {{x\left( {x - 3} \right) + 2\left( {x - 3} \right) + 8} \over {x - 3}} \cr 
& = {{\left( {x - 3} \right)\left( {x + 2} \right) + 8} \over {x - 3}} \cr 
& = x + 2 + {8 \over {x - 3}} \cr} \)

Để  \(\dfrac{{{x^2} - x + 2}}{{x - 3}}\) là nguyên thì \(\dfrac{8}{{x - 3}}\) phải nguyên. Suy ra \(x - 3\) là ước của \(8.\)

Các ước của \(8\) là \( \pm 1, \pm 2, \pm 4, \pm 8\).

Do đó \( x-3 \in \{ -8; \; -4;\; -2; \;-1; \;1;\;2;\;4; \; 8 \}\).

Ta có bảng sau:

Vậy \(x \in \{  - 5;\; - 1;\; 1; \;2;\;4;\; 5;\;7;\; 11\}\).

HocTot.Nam.Name.Vn